为推进节能减排，发展低碳经济，江阴某公司以25万元购得某项节能产品的生产技术后，再投入100万元购买生产设备，进行该产品的生产加工．已知生产这种产品的成本价为每件20元．经过市场调研发现，该产品的销售单价定在25元到30元之间较为合理，并且该产品的年销售量y（万件）与销售单价x（元）之间的函数关系式为：
（年获利=年销售收入—生产成本—投资成本）
（1）当销售单价定为28元时，该产品的年销售量为多少万件？
（2）求该公司第一年的年获利W（万元）与销售单价x（元）之间的函数关系式，并说明投资的第一年，该公司是盈利还是亏损？若盈利，最大利润是多少？若亏损，最小亏损是多少？
（3）第二年，该公司决定给希望工程捐款Z万元，该项捐款由两部分组成：一部分为10万元的固定捐款；另一部分则为每销售一件产品，就抽出一元钱作为捐款．若除去第一年的最大获利（或最小亏损）以及第二年的捐款后，到第二年年底，两年的总盈利不低于67．5万元，请你确定此时销售单价的范围．
已知函数
与函数
交于点A（2，b）B（-3，m）两点（点A在第一象限），
|
与x轴交于点C，求△ABC的面积．
（本小题满分7分）甲、乙两人沿同一路线登山，图中线段
、折线
分别是甲、乙两人登山的路程
（米）与登山时间
之间的函数图象．请根据图象所提供的信息，解答如下问题： 
（1）求甲登山的路程与登山时间之间的函数关系式，并写出自变量的取值范围；
（2）求乙出发后多长时间追上甲？此时乙所走的路程是多少米？
如图1所示，某乘客乘高速列车从甲地经过乙地到丙地，列车匀速行驶，图2为列车离乙地路程y（千米）与行驶时间x（小时）时间的函数关系图象．
（1）填空：甲、丙两地距离 千米．
（2）求高速列车离乙地的路程y与行驶时间x之间的函数关系式，并写出x的取值范围．
如图，在方格纸中（小正方形的边长为1），反比例函数
与直线的交点A、B均在格点上，根据所给的直角坐标系（O是坐标原点），解答下列问题：
（1）①分别写出点A、B的坐标；
②把直线AB向右平移5个单位，再向上平移5个单位，求出平移后直线A′B′的解析式；
（2）若点C在函数的图象上，△ABC是以AB为底的等腰三角形，请写出点C的坐标．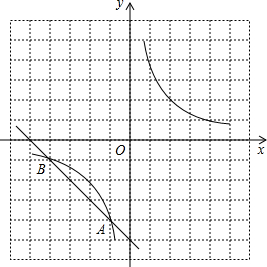
如图，在平面直角坐标系中，一次函数y=2x+b的图象与反比例函数y=
（k≠0）的图象交于A、B两点，与x轴交于点C（-2，0），点A的坐标为（n，6）．
（1）求该反比例函数的解析式；
（2）求点B的坐标，写出正比例函数值大于反比例函数值时自变量x的取值范围；
（3）若点E为x轴上使△ACE为直角三角形的一点，求点E的坐标．
【实际情境】
某中学九年级学生步行到郊外春游．一班的学生组成前队，速度为4km/h，二班的学生组成后队，速度为6km/h．前队出发1h后，后队才出发，同时，后队派一名联络员骑自行车在两队之间不间断地来回进行联络，他骑车的速度为12km/h．
【数学研究】
若不计队伍的长度，如图，折线A-B-C、A-D-E分别表示后队、联络员在行进过程中，离前队的路程y（km）与后队行进时间x（h）之间的部分函数图象．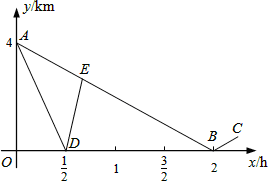
（1）求线段AB对应的函数关系式；
（2）求点E的坐标，并说明它的实际意义；
（3）联络员从出发到他折返后第一次与后队相遇的过程中，当x为何值时，他离前队的路程与他离后队的路程相等？
随着信息技术的快速发展，“互联网+”渗透到我们日常生活的各个领域，网上在线学习交流已不再是梦，现有某教学网站策划了A，B两种上网学习的月收费方式：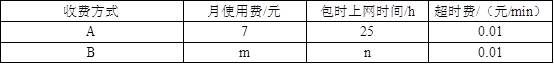
设每月上网学习时间为x小时，方案A，B的收费金额分别为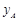
，
．
（1）如图是与x之间函数关系的图象，请根据图象填空：m= ；n= ；
（2）写出与x之间的函数关系式．
（3）选择哪种方式上网学习合算，为什么？
某商场欲购进果汁饮料和碳酸饮料共50箱，果汁饮料毎箱进价为55元，售价为63元；碳酸饮料毎箱进价为36元，售价为42元；设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注，总利润=总售价﹣总进价），
（1）设商场购进碳酸饮料y箱，直接写出y与x的函数关系式；
（2）求总利润w关于x的函数关系式；
（3）如果购进两种饮料的总费用不超过2000元，那么该商场如何进货才能获利最多？并求出最大利润．
某商场购进一批单价为4元的日用品．若按每件5元的价格销售，每月能卖出300件；若按每件6元的价格销售，每月能卖出200件，假定每月销售件数y（件）与价格x（元/件）之间满足一次函数关系．
（1）试求y与x之间的函数关系式；
（2）当销售价格定为多少时，才能使每月的利润最大？每月的最大利润是多少？
为奖励在演讲比赛中获奖的同学，班主任派学习委员小明为获奖同学买奖品，要求每人一件．小明到文具店看了商品后，决定奖品在钢笔和笔记本中选择．如果买4个笔记本和2支钢笔，则需86元；如果买3个笔记本和1支钢笔，则需57元．
（1）求购买每个笔记本和钢笔分别为多少元？
（2）售货员提示，买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受8折优惠，若买x（x＞0）支钢笔需要花y元，请你求出y与x的函数关系式；
（3）在（2）的条件下，小明决定买同一种奖品，数量超过10个，请帮小明判断买哪种奖品省钱．
某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按120个工时计算）生产空调器、彩电、冰箱共360台，且冰箱至少生产60台，已知生产这些家电产品每台所需工时和每台产值如下表：
| 家电名称 |
空调 |
彩电 |
冰箱 |
||||||
| 工 时 |
|
|
|
||||||
| 产值（千元） |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？（以千元为单位）
一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量有两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示．
（1）当4≤x≤12时，求y关于x的函数解析式；
（2）直接写出每分进水，出水各多少升．
开学初，小明到文具批发部一次性购买某种笔记本，该文具批发部规定：这种笔记本售价y（元/本）与购买数量x（本）之间的函数关系如图所示．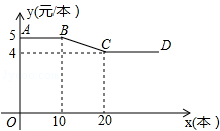
（1）图中线段AB所表示的实际意义是 ；
（2）请直接写出y与x之间的函数关系式；
（3）已知该文具批发部这种笔记本的进价是3元/本，若小明购买此种笔记本超过10本但不超过20本，那么小明购买多少本时，该文具批发部在这次买卖中所获的利润W（元）最大？最大利润是多少？
一农民带上若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的土豆千克数与他手中持有的钱数（含备用零钱）的关系，如图所示，结合图象回答下列问题．
（1）农民自带的零钱是多少？
（2）试求降价前y与x之间的关系式？
（3）由表达式你能求出降价前每千克的土豆价格是多少？
（4）降价后他按每千克0．4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，试问他一共带了多少千克土豆？
粤公网安备 44130202000953号
