初中数学一次函数的最值解答题

某商场购进一种单价为元的篮球，如果以单价元售出，那么每天可售出50个．根据销售经验，售价每提高元．销售量相应减少1个。
（1）假设销售单价提高元，那么销售每个篮球所获得的利润是_____元；这种篮球每天的销售量是_________个。
（2）假设每天销售这种篮球所得利润为y ,请用含的代数式表示y。
（3）假如你是商场老板，为了在出售这种篮球时获得最大利润，你该提高多少元？最大利润是多少？请说明理由。

如图，已知直线y=x+1与y轴交于点A，一次函数y=kx+b的图象经过点B（0，-1），并且与x轴以及直线y=x+1分别交于点C、D．

（1）求直线BD的函数表达式；
（2）求四边形AOCD的面积；
（3）在y轴上是否存在这样的点P，使得以P、B、D为顶点的三角形是等腰三角形．如果存在，求出点P的坐标；如果不存在，说明理由．

如图，直线y = kx+6与x轴y轴分别相交于点E，F。点E的坐标为（- 8，0），点A的坐标为（- 6，0）。 点P（x，y）是第二象限内的直线上的一个动点。

（1）求k的值；
（2）当点P运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
（3）探究：当P运动到什么位置（求P的坐标）时，△OPA的面积为，并说明理由

已知y与x-3成正比例，当x=4时，y=3；
（1）求y与x的函数式；
（2）当x=2时，求y的值．

如图所示，直线与x轴、y轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处

求（1）点B′、M的坐标
（2）直线AM的解析式。

小轿车从甲地出发驶往乙地，同时货车从相距乙地60km的入口处驶往甲地（两车均在甲、乙两地之间的公路上匀速行驶），如图是它们离甲地的路程y（km）与货车行驶时间x（h）之间的函数的部分图象．

（1）求货车离甲地的路程y（km）与它的行驶时间x（h）的函数关系式；
（2）哪一辆车先到达目的地？说明理由．

如图，已知点是一次函数图象与反比例函数图象的一个交点．
（1）求一次函数的解析式；
（2）在y轴的右侧，当时，直接写出的取值范围．

如图①，△OAB中，A（0，2），B（4，0），将△AOB向右平移m个单位，得到△O′A′B′．
（1）当m=4时，如图②．若反比例函数y =的图象经过点A′，一次函数y=ax+b的图象经过A′、B′两点．求反比例函数及一次函数的表达式；
（2）若反比例函数y=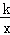的图象经过点A′及A′B′的中点M，求m的值．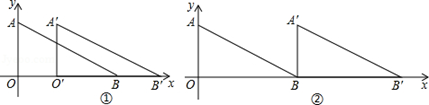

已知关于x的一次函数y＝mx＋2的图像经过点（－2，6）．
（1）求m的值；
（2）画出此函数的图像；

“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．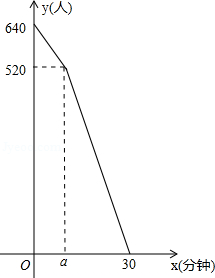

（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

已知一次函数y=kx+b的图象经过点（﹣1，﹣5），且与正比例函数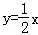的图象相交于点（2，m）．
求：（1）m的值；     
（2）一次函数y=kx+b的解析式；
（3）这两个函数图象与x轴所围成的三角形面积．

“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．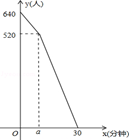

（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

国庆长假，小明从老家乘车去上海．一路上，小明记下了如下数据（注：“上海90km”表示离上海的距离为90km）：

观察时间	10：30（t=0）	10：36（t=6）	10：30（t=18）
路牌内容	上海90Km	上海80Km	上海60Km

 
假设汽车离上海的距离s（km）是行驶时间t（min）的一次函数，求s关于t的函数关系式．

已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数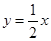的图象相交于点（2，a）．
（1）求a的值．
（2）求一次函数y=kx+b的表达式．
（3）在同一坐标系中，画出这两个函数的图象．

自2012年6月1日起，全国实施了阶梯电价．某省出台了阶梯电价方案：电价分“三档”收费，第一档为a度，居民用电量低于a度的部分，执行现行的标准电价（0．53元/度）；第二档为a～b度，居民月用电量在a～b之间的部分，电价在一档电价的基础上提高0．05元/度；第三档为超过b度，居民月用电量高于b度的部分，电价在一档电价的基础上提高m元/度．实施阶梯电价后，月电费y（元）与月用电量x（度）之间的函数关系如图所示．

（1）求a，b，m的值；
（2）求y与x之间函数关系式，并写出自变量x的取值范围．