甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下.将图中( )填上适当的值,并求甲车从A到B的速度.
求从甲车返回到与乙车相遇过程中y与x的函数关系式,并写出自变量取值范围.
求出甲车返回时行驶速度及AB两地的距离.

如图,在平面直角坐标系中,一次函数y=2x+b的图象与反比例函数y= (k≠0)的图象交于A、B两点,与x轴交于点C(-2,0),点A的坐标为(n,6).
(k≠0)的图象交于A、B两点,与x轴交于点C(-2,0),点A的坐标为(n,6).
(1)求该反比例函数的解析式;
(2)求点B的坐标,写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若点E为x轴上使△ACE为直角三角形的一点,求点E的坐标.
“五一”期间,为了满足广大人民的消费需求,某商店计划用160 000元购进一批家电,这批家电的进价和售价如下表:
若全部资金用来购买彩电和洗衣机共100台,则商家可以购买彩电和洗衣机各几台?
若在现有资金160 000元允许的范围内,购买上表中三类家电共100台,其中彩电台数和冰箱台数相同,且购买洗衣机的台数不超过购买彩电的台数,请你算一算,共有几种进货方案?哪种进货方案能使商店销售完这批家电后获得的利润最大?并求出最大利润.(利润=售价-进价)
4月20日8时2分,四川省雅安市芦山县发生了7.0级地震,当地的部分房屋严重受损,上万灾民无家可归,灾情牵动亿万中国人的心。某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资。已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
| 车 型 运往地 |
甲 地(元/辆) |
乙 地(元/辆) |
| 大货车 |
720 |
800 |
| 小货车 |
500 |
650 |
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为 辆,前往甲、乙两地的总运费为w元,求出w与
辆,前往甲、乙两地的总运费为w元,求出w与 的函数关系式(写出自变量的取值范围);
的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费
某市出租车5㎞内(包括5㎞)起步价为8元,以后每增加1㎞加价2元(不足1㎞按1㎞计),请写出乘坐出租车路程x㎞(x为整数)与收费y元的函数关系式,并计算小明乘了10㎞要付多少钱?
小丽一家利用元旦三天驾车到某景点旅游。小汽车出发前油箱有油36L,行驶若干h后,途中在加油站加油若干L。油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示。根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目的地,油箱中的油是否够用?请说明理由.
如图,一次函数的图象与反比例函数 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.
(1)求一次函数的解析式;
(2)设函数 (x>0)的图象与
(x>0)的图象与 (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在 (x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
(x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
如图,直线l:y= x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.

(1)点A坐标是 ,点B的坐标 ,BC= .
(2)当点P在什么位置时,△APQ≌△CBP,说明理由.
(3)当△PQB为等腰三角形时,求点P的坐标.
如图,已知一次函数 的图象与反比例函数
的图象与反比例函数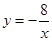 的图象交于
的图象交于 ,
, 两点,且点
两点,且点 的横坐标和
的横坐标和 点的纵坐标都是
点的纵坐标都是 .
.
求:(1)一次函数解析式;
(2)求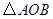 的面积.
的面积.
开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.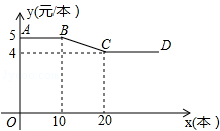
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
(本小题12分)如图,直线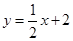 分别交轴于
分别交轴于 、
、 ,点
,点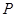 是该直线与反比例函数在第一象限内的一个交点,
是该直线与反比例函数在第一象限内的一个交点,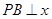 轴于
轴于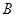 ,且
,且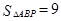 .
.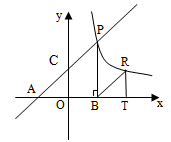
(1)求点 的坐标;
的坐标;
(2)设点 与点
与点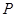 在同一个反比例函数的图象上,且点
在同一个反比例函数的图象上,且点 在直线
在直线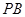 的右侧,作
的右侧,作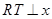 轴于
轴于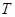 ,当
,当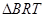 与
与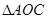 相似时,求点
相似时,求点 的坐标.
的坐标.
如图,反比例函数 与一次函数y=x+b的图象,都经过点A(1,2)
与一次函数y=x+b的图象,都经过点A(1,2)
(1)试确定反比例函数和一次函数的解析式;
(2)求一次函数图象与两坐标轴的交点坐标.