初中数学一次函数的最值解答题

重庆市垫江县具有2000多年的牡丹种植历史．每年3月下旬至4月上旬，主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放，美不胜收．由于牡丹之根———丹皮是重要中药材，目前已种植有60多个品种2万余亩牡丹的垫江，因此成为我国丹皮出口基地，获得“丹皮之乡”的美誉。为了提高农户收入，该县决定在现有基础上开荒种植牡丹并实行政府补贴，规定每新种植一亩牡丹一次性补贴农户若干元，经调查，种植亩数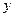(亩)与补贴数额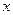(元)之间成一次函数关系，且补贴与种植情况如下表：

补贴数额(元)	10	20	……
种植亩数(亩)	160	240	……

随着补贴数额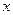的不断增大，种植规模也不断增加，但每亩牡丹的收益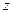(元)会相应降低，且该县补贴政策实施前每亩牡丹的收益为3000元，而每补贴10元(补贴数为10元的整数倍)，每亩牡丹的收益会相应减少30元．
(1)分别求出政府补贴政策实施后，种植亩数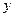(亩)、每亩牡丹的收益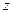(元)与政府补贴数额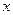(元)之间的函数关系式；
(2)要使全县新种植的牡丹总收益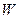(元)最大，又要从政府的角度出发，政府应将每亩补贴数额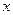定为多少元？并求出总收益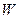的最大值和此时种植亩数；(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下，为了发展旅游业，需占用其中不超过50亩的新种牡丹园，利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”．已知引进该新品种平均每亩的费用为530元，此外还要购置其它设备，这项费用(元)等于种植面积(亩)的平方的25倍．这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元，这部分混种土地在扣除所有费用后总收益为85000元．求混种牡丹的土地有多少亩？(结果精确到个位)(参考数据：)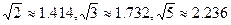

已知一次函数

①在给定的直角坐标系中作出它的图象；
②此函数图象与x轴、y轴的交点A、B坐标分别为______；______。
③函数图象与坐标轴围成的三角形的周长是多少？

生活中，有人喜欢把传送的便条折成形状，折叠过程是这样的（阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为，宽为，分别回答下列问题：

（1）为了保证能折成图④的形状（即纸条两端均超出点），试求的取值范围．
（2）如果不但要折成图④的形状，而且为了美观，希望纸条两端超出点的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点与点的距离（用表示）

康乐公司在两地分别有同型号的机器台和台，现要运往甲地台，乙地台，从两地运往甲、乙两地的费用如下表：

	甲地（元／台）	乙地（元／台）
地
地

（1）如果从地运往甲地台，求完成以上调运所需总费用（元）与（台）之间的函数关系式；
（2）请你为康乐公司设计一种最佳调运方案，使总费用最少，并说明理由

一次函数y=kx+b图象经过点（1，3）和（4，6）。

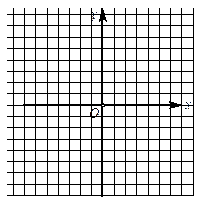
①试求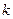与；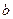
②画出这个一次函数图象；
③这个一次函数与y轴交点坐标是（　　　）
④当x    时，y=0； 
⑤当x    时，y﹥0；

甲、乙两班参加植树活动．乙班先植树30棵，然后甲班才开始与乙班一起植树．设甲班植树的总量为（棵），乙班植树的总量为（棵），两班一起植树所用的时间（从甲班开始植树时计时）为（时），、分别与之间的部分函数图象如图9所示．

（1）当0≤x≤6时，分别求、与之间的函数关系式；
（2）如果甲、乙两班均保持前6个小时的工作效率，通过计算说明，当时，甲、乙两班植树的总量之和能否超过棵．

已知函数y="(k+1)x" + k-1．
（1）若函数的图象经过原点，求k的值；
（2）若函数的图象经过第一、三、四象限，求k的取值范围．

已知一次函数的图像经过点（－2，5），并且与直线=3－4相交于轴上，求此函数的解析式

如图，直线与双曲线相交于A（2，1）、B两点．

（1）求m及k的值；
（2）不解关于x、y的方程组直接写出点B的坐标；
（3）直线经过点B吗？请说明理由．

有一种螃蟹，从海上捕获后不放养，最多只能存活两天.如果放养在塘内，可以延长存活时间，但每天也有一定数量的蟹死去.假设放养期内蟹的个体质量基本保持不变，现有一经销商，按市场价收购这种活蟹1000 kg放养在塘内，此时市场价为每千克30元，据测算，此后每千克活蟹的市场价每天可上升1元，但是，放养一天需支出各种费用为400元，且平均每天还有10 kg蟹死去，假定死蟹均于当天全部销售出，售价都是每千克20元.
(1)设x天后每千克活蟹的市场价为p元，写出p关于x的函数关系式;
(2)如果放养x天后将活蟹一次性出售，并记1000 kg蟹的销售总额为Q元，写出Q关于x的函数关系式.
(3)该经销商将这批蟹放养多少天后出售，可获最大利润(利润=Q－收购总额)？

如图12-1，已知直线y= -x+4交x轴于点A，交y轴于点B．

（1）写出A、B两点的坐标分别是：                                ；
（2）设点P是射线y = x（）上一点，点P的横坐标为t，M是OP的中点（O是原点），以PM为对角线作正方形PDME．正方形PDME与△OAB公共部分的面积为S，求S与t之间的函数关系式，并求S的最大值．（图12-2、12-3供你探索问题时使用）