如图12-1，已知直线y= -x+4交x轴于点A，交y轴于点B．
（1）写出A、B两点的坐标分别是： ；
（2）设点P是射线y = x（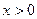
）上一点，点P的横坐标为t，M是OP的中点（O是原点），以PM为对角线作正方形PDME．正方形PDME与△OAB公共部分的面积为S，求S与t之间的函数关系式，并求S的最大值．（图12-2、12-3供你探索问题时使用）
是方程
的两个不相等的实数根，（1）求
的值
的值
的方程
，求另一个根及
值．
相关知识点
推荐套卷
如图12-1，已知直线y= -x+4交x轴于点A，交y轴于点B．
（1）写出A、B两点的坐标分别是： ；
（2）设点P是射线y = x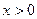（）上一点，点P的横坐标为t，M是OP的中点（O是原点），以PM为对角线作正方形PDME．正方形PDME与△OAB公共部分的面积为S，求S与t之间的函数关系式，并求S的最大值．（图12-2、12-3供你探索问题时使用）
粤公网安备 44130202000953号