一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为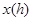 ,两车之间的距离为
,两车之间的距离为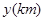 ,图中的折线表示
,图中的折线表示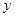 与
与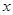 之间的函数关系.
之间的函数关系.
根据图象进行以下探究
(1)请解释图中点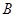 的实际意义;
的实际意义;
(2)求慢车和快车的速度;
(3)求线段BC所表示的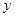 与
与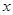 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量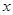 的取值范围;
的取值范围;
解答题:声音在空气中传播的速度 (m/s)是气温
(m/s)是气温 (℃)的一次函数,下表列出了一组不同气温的音速:
(℃)的一次函数,下表列出了一组不同气温的音速:
气温 (℃) (℃) |
0 |
5 |
10 |
15 |
20 |
音速 (m/s) (m/s) |
331 |
334 |
337 |
340 |
343 |
(1)求 与
与 之间的函数关系式;(2)气温
之间的函数关系式;(2)气温 ℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
如图,在方格纸中(小正方形的边长为1),反比例函数 与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)①分别写出点A、B的坐标;
②把直线AB向右平移5个单位,再向上平移5个单位,求出平移后直线A′B′的解析式;
(2)若点C在函数 的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.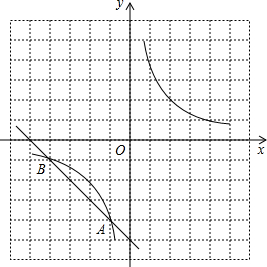
在平面直角坐标系中,一次函数的图象与坐标轴围成的三 角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
求函数y=
 x+3的坐标三角形的三条边长;
x+3的坐标三角形的三条边长;若函数y=
 x+b(b为常数)的坐标三角形周长为16,
x+b(b为常数)的坐标三角形周长为16,
求此三角形面积.
(8分)如图,一直线BC与已知直线AB: 关于y轴对称。
关于y轴对称。
(1)求直线BC的解析式;
(2)说明两直线与x轴围成的三角形是等腰三角形。
(本题满分12分)某商场购进一批单价为16元日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数Y(件)是价格X(元/件)的一次函数 (1)试求Y 与X之间的关系式。
(2)在商品积压,且不考虑其它因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本)
如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数 (
( )的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(1)求点A的坐标及一次函数解析式.
(2)求点C的坐标及反比例函数的解析式.
如图,直线l:y= x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.

(1)点A坐标是 ,点B的坐标 ,BC= .
(2)当点P在什么位置时,△APQ≌△CBP,说明理由.
(3)当△PQB为等腰三角形时,求点P的坐标.
如图,已知一次函数 的图象与反比例函数
的图象与反比例函数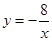 的图象交于
的图象交于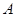 ,
, 两点,且点
两点,且点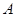 的横坐标和
的横坐标和 点的纵坐标都是
点的纵坐标都是 .
.
求:(1)一次函数解析式;
(2)求 的面积.
的面积.
开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.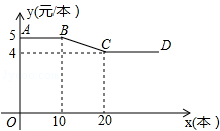
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
(本小题12分)如图,直线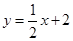 分别交轴于
分别交轴于 、
、 ,点
,点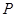 是该直线与反比例函数在第一象限内的一个交点,
是该直线与反比例函数在第一象限内的一个交点,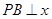 轴于
轴于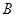 ,且
,且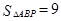 .
.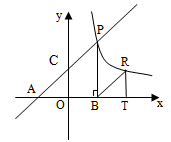
(1)求点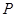 的坐标;
的坐标;
(2)设点 与点
与点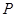 在同一个反比例函数的图象上,且点
在同一个反比例函数的图象上,且点 在直线
在直线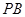 的右侧,作
的右侧,作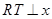 轴于
轴于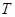 ,当
,当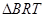 与
与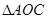 相似时,求点
相似时,求点 的坐标.
的坐标.
如图,反比例函数 与一次函数y=x+b的图象,都经过点A(1,2)
与一次函数y=x+b的图象,都经过点A(1,2)
(1)试确定反比例函数和一次函数的解析式;
(2)求一次函数图象与两坐标轴的交点坐标.