经统计分析.某市跨河大桥上的车流速度v(千米/时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞.此时车流速度为0千米/时;当车流密度不超过20辆/千米,车流速度为80千米/时.研究表明:当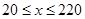 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度;
(2)在某一交通时段.为使大桥上的车流速度大于60千米/时且小于80千米/时,应把大桥上的车流密度控制在什么范围内?
(本小题满分12分)如图,在直角坐标系xOy中,一次函数 (m为常数)的图像与x轴交于A(-3,0),与y轴交于点C;以直线
(m为常数)的图像与x轴交于A(-3,0),与y轴交于点C;以直线 为对称轴的抛物线
为对称轴的抛物线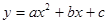 (a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.
(a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.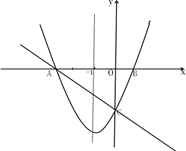
(1)求一次函数及抛物线的函数表达式。
(2)在对称轴上是否存在一点P,使得 PBC的周长最小,若存在,请求出点P的坐标.
PBC的周长最小,若存在,请求出点P的坐标.
(3)点D是线段OC上的一个动点(不与点O、点C重合),过点D作DE‖PC交x轴于点E,连接PD、PE。设CD的长为m,  PDE的面积为S。求S与m之间的函数关系式。并说明S是否存在最大值,若存在,请求出最大值:若不存在,请说明理由。
PDE的面积为S。求S与m之间的函数关系式。并说明S是否存在最大值,若存在,请求出最大值:若不存在,请说明理由。
甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.
(1)写出乙船在逆流中行驶的速度;
(2)求甲船在逆流中行驶的路程;
(3)求甲船到A港的距离y1与行驶时间x之间的函数关系式;
(4)求救生圈落入水中时,甲船到A港的距离.
王先生开轿车从A地出发,前往B地,路过服务区休息一段时间后,继续以原速度行驶,到达B地后,又休息了一段时间,然后开轿车按原路返回A地,速度是原来的1.2倍.王先生距离A地的路程y(km)与行驶的时间x(h)之间的函数图象如图所示.
(1)王先生开轿车从A地行驶到B地的途中,休息了 h;
(2)求王先生开轿车从B地返回A地时y与x之间的函数关系式(不要求写出自变量x的取值范围);
(3)王先生从B地返回A地的途中,再次经过从A地到B地时休息的服务区,求此时的x的值.
如图,已知反比例函数 的图象与一次函数
的图象与一次函数 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,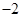 ).
).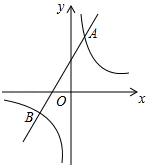
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
如图,反比例函数 与正比例函数y=ax相交于A(1,k),B(-k,-1)两点。
与正比例函数y=ax相交于A(1,k),B(-k,-1)两点。
(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数y=ax的图象平移,得到一次函数y=ax+b的图象,与函数 的图象交于C(x1,y1)、D(x2,y2),且|x1-x2|·|y1-y2|=5,求b的值。
的图象交于C(x1,y1)、D(x2,y2),且|x1-x2|·|y1-y2|=5,求b的值。
大星发超市进了一批成本为8元/个的文具盒。调查发现:这种文具盒每个星期的销售量y(个)与它的定价x(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销售量y(个)与它的定价x(元/个)之间的函数关系式(不必写出自变
量x的取值范围);
(2)每个文具盒定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润最高?最高利润是多少?
某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是_______元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;
(2)设每月用水量为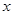 吨,应交水费为
吨,应交水费为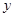 元,写出
元,写出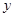 与
与 之间的函数关系式;
之间的函数关系式;
(3)小黄家3月份用水26吨,他家应交水费多少元?
已知如图,在平面直角坐标系中,一次函数 =
=
 +b(
+b( ≠0)的图象与反比例函数
≠0)的图象与反比例函数 =
= (
( ≠0)的图象交于一、三象限内A、B两点,与
≠0)的图象交于一、三象限内A、B两点,与 轴交于点C;点A(2,m),点B(n,-2),且t
轴交于点C;点A(2,m),点B(n,-2),且t n∠Boc=
n∠Boc= ;
;
(1)求一次函数和反比例函数的解析式;
(2)在 轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求点E的坐标。
轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求点E的坐标。
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图像与反比例函数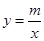 (m≠0)的图像交于A,B两点,与x轴交于点C,点A的坐标为(n,6),点C的坐标为(-2,0)且tan∠ACO=2.
(m≠0)的图像交于A,B两点,与x轴交于点C,点A的坐标为(n,6),点C的坐标为(-2,0)且tan∠ACO=2.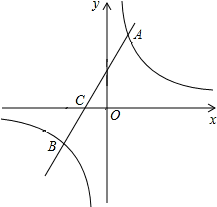
(1)求反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形(直接写出点E的坐标)
甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)与清雪时间x(时)之间的函数图象如图所示.
(1)乙队调离时,甲、乙两队已完成的清雪总量为 吨;
(2)求此次任务的清雪总量 ;
;
(3)求乙队调离后y与x之间的函数关系式.
如图,直线y= x+2与x轴、y轴分别交于A、B两点,点C的坐标为(﹣3,0),P(x,y)是直线y=
x+2与x轴、y轴分别交于A、B两点,点C的坐标为(﹣3,0),P(x,y)是直线y= x+2的一个动点(点P不与点A重合).
x+2的一个动点(点P不与点A重合).
(1)在点P运动过程中,试写出△OPC的面积S与x的函数关系式;
(2)当P运动到什么位置时,△OPC的面积为 ,求出此时点P的坐标;
,求出此时点P的坐标;
(3)过P作AB的垂线分别交x轴、y轴于E、F两点,是否存在这样的点P,使△EOF≌△BOA?若存在,求出点P的坐标;若不存在,请说明理由.
已知函数y=kx+b的图象经过点A(- 3, - 2)及点B(1, 6).
(1)求此一次函数解析式,并画图象; (2)求函数y=2x+4图象与坐标轴围成的三角形的面积.
如图,已知直线 :
: 与直线
与直线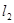 :y = mx-4m的图像的交点C 在第四象限,且点C到y轴的距离为2.
:y = mx-4m的图像的交点C 在第四象限,且点C到y轴的距离为2.
(1)求直线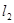 的解析式;
的解析式;
(2)求△ADC的面积;
(3)在第一象限的角平分线上是否存在点P,使得△ADP的面积是△ADC的面积的2倍?如果存在,求出点P的坐标,如果不存在,请说明理由.