初中数学一次函数的最值选择题

已知一次函数y=x+b的图象经过第一、二、三象限，则b的值可以是(    ).

A．－2

B．－1

C．0

D．2

一个矩形被直线分成面积为，的两部分，则与之间的函数关系只可能是

.当k>0时，正比例函数y=kx的图象大致是（  ）

一个正常人在做激烈运动时，心跳速度加快，当运动停止下来后，心跳次数N(次)与时间s(分)的函数关系图像大致是  （     ）

如图，是张老师出门散步时离家的距离与时间之间的函数关系的图象，若用
黑点表示张老师家的位置，则张老师散步行走的路线可能是

在平面直角坐标系中，把直线向左平移一个单位长度后，其直线解析式为（　　）

A．

B．

C．

D．

小高从家骑自行车去学校上学，先走上坡路到达点A，再走下坡路到达点B，最后走平路到达学校，所用的时间与路程的关系如图所示．放学后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上学时一致，那么他从学校到家需要的时间是（　　）

A．14分钟

B．17分钟

C．18分钟

D．20分钟

如图3，小红居住的小区内有一条笔直的小路，小路的正中间有一路灯，晚上小红由A处径直走到B处，她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来，大致图象是

如图，已知直线l：y=x，过点A（0，1）作y轴的垂线交直线l于点B，过
点B作直线l的垂线交y轴于点A₁；过点A₁作y轴的垂线交直线l于点B₁，过点B₁作直线l的垂线交y轴于点A₂；…；按此作法继续下去，则点A₄的坐标为

A．（0，64）

B．（0，128）

C．（0，256）

D．（0，512）

将直线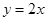向右平移l个单位后所得图象对应的函数解析式为

A．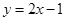

B．

C．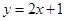

D．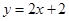

小亮从家步行到公交车站台，等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A．他离家8km共用了30min	B．他等公交车时间为6min
C．他步行的速度是100m/min	D．公交车的速度是350m/min

如图，正方形 $ABCD$的边长为4， $P$为正方形边上一动点，运动路线是 $A\to D\to C\to B\to A$,设 $P$点经过的路程为 $x$，以点 $A$、 $P$、 $D$为顶点的三角形的面积是 $y$.则下列图象能大致反映 $y$与 $x$的函数关系的是(     )

A．		B．
C．		D．

如图，在平面直角坐标系中，□OABC的顶点A在轴上，顶点B的坐标为
（6，4）．若直线l经过点（1，0），且将□OABC分割成面积相等的两部分，则直线l的函
数解析式是（   ）

A．	B．
C．	D．

已知直线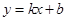经过点(k，3)和(1，k)，则k的值为(   )

A．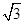

B．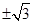

C．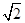

D．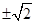

甲、乙两人沿相同的路线由A地到B地匀速前进，A、B两地间的路程为20km．他们前进的路程为s(km)，甲出发后的时间为t(h)，甲、乙前进的路程与时间的函数图象如图所示．根据图象信息，下列说法正确的是【   】

A．甲的速度是4km/h	B．乙的速度是10km/h
C．乙比甲晚出发1h	D．甲比乙晚到B地3h