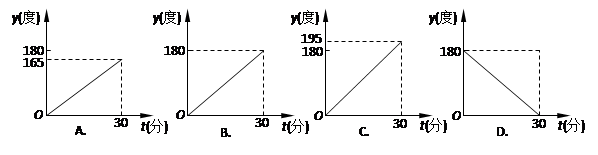初中数学一次函数的最值选择题

某储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开始调出
物资（调进物资与调出物资的速度均保持不变）．储运部库存物资S(吨)与时间t (小时)之间
的函数关系如图所示，这批物资从开始调进到全部调出需要的时间是        （    ）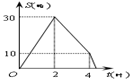

A．4小时

B．4.4小时

C．4.8小时

D．5小时

函数y=(2m－1)x是正比例函数，且y随自变量x的增大而增大，则m的取值范围是                                              

A．m>

B．m<

C．m≥

D．m≤

一次函数的图象大致是(    ).

下列四个点，在正比例函数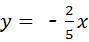的图象上的点是（　　）

A．（2，5）	B．（5，2）
C．（2，﹣5）	D．（5，﹣2

小华同学利用假期时间乘坐一大巴去看望在外打工的妈妈，出发时，大巴的油箱装满了油，匀速行驶一段时间后，油箱内的汽油恰剩一半时又加满了油，接着按原速度行驶，到目的地时油箱中还剩有箱汽油，设油箱中所剩汽油量为V升，时间为t（分钟），则V与t的大致图象是（　　）

如图，在平面直角坐标系中，直线 $y=\frac{2}{3} x－\frac{2}{3}$与矩形
$ABCD$的边 $OC$、 $BC$分别交于点 $E$、 $F$，已知 $OA=3$， $OC=4$，则 $△CEF$的面积是

（A）6          （B）3           （C）12            （D）

两条直线 $y=k_{2}x+b_1$和 $y=k_{2}x+b_2$ 相交于点A(－2,3),侧方程组 $\left\{\begin{array}{l}y=k_{1}x+b_1\\ y=k_{2}x+b_2\end{array}\right.$的解是
A $\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$   B $\left\{\begin{array}{l}x=-2\\ y=3\end{array}\right.$     C $\left\{\begin{array}{l}x=3\\ y=-2\end{array}\right.$   D $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$

（11·肇庆）某住宅小区六月份1日至5日母天用水量变化情况如图4所示．那么
这5天平均母天的用水量是

A．30吨

B．31吨

C．32吨

D．33吨

如图，在圆锥形的稻草堆顶点 $P$处有一只猫，看到底面圆周上的点 $A$处有一只老鼠，猫沿着母线 $PA$下去抓老鼠，猫到达点 $A$时，老鼠已沿着底面圆周逃跑，猫在后面沿着相同的路线追，在圆周的点 $B$处抓到了老鼠后沿母线 $BP$回到顶点 $P$处．在这个过程中，假设猫的速度是匀速的，猫出发后与点P距离 $s$，所用时间为 $t$，则 $s$与 $t$之间的函数关系图象是

A．		B．
C．		D．

如图，直线l：y＝x＋2与y轴交于点A，将直线l绕点A旋转90º后，所得直
线的解析式为【   】

A．y＝x－2	B．y＝－x＋2
C．y＝－x－2	D．y＝－2x－1

已知一次函数的图象过第一、二、四象限，且与x轴交于点（2，0），则关于的不等式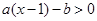的解集为

A．

B．

C．

D．

如图，已知A点坐标为（5，0），直线与y轴交于点B，连接AB，∠a=75°，则b的值为

A．3

B．

C．4

D．

关于一次函数y=﹣x+1的图象，下列所画正确的是（　　）

A．	B．
C．	D．

如图，已知直线l：y=x，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A₁；过点A₁作y轴的垂线交直线l于点B₁，过点B₁作直线l的垂线交y轴于点A₂；…；按此作法继续下去，则点A₄的坐标为（　　）

A．（0，64）	B．（0，128）
C．（0，256）	D．（0，512）

时钟在正常运行时，分针每分钟转动6°，时针每分钟转动0.5°.在运行过程中，时针与分针的夹角会随着时间的变化而变化.设时针与分针的夹角为y(度)，运行时间为t(分)，当时间从12︰00开始到12︰30止，y与 t之间的函数图象是（   ）.