2011年初中毕业升学考试(广西梧州卷)数学
(11·佛山)若⊙O的一条弧所对的圆周角为60°,则这条弧所对的圆心角是( )
| A.30° | B.60° | C.120° | D.以上答案都不对 |
(11·佛山)在①a4·a2;②(-a 2)3;③a12÷a2;④a2·a3中,计算结果为a6的个数是()
| A.1个 | B.2个 | C.3个 | D.4个 |
(11·佛山)一个图形无论经过平移还是旋转,有以下说法( )
①对应线段平行; ②对应线段相等;
③对应角相等; ④图形的形状和大小都没有发生变化
| A.①②③ | B.①②④ | C.①③4 | D.②③④ |
(11·佛山)如图,一个小立方块所搭的几何体,从不同的方向看所得到的平面图形中(小正方形中的数字表示在该位置的小立方块的个数),不正确的是( )
(11·佛山)下列说法正确的是( )
| A.“作线段CD=AB”是一个命题; |
| B.三角形的三条内角平分线的交点为三角形的内心; |
| C.命题“若x=1,则x2=1”的逆命题是真命题; |
| D.“具有相同字母的项称为同类项”是“同类项”的定义; |
(11·佛山)某生数学科课堂表现为90分、平时作业为92分、期末考试为85分,
若这三项成绩分别按 、
、 、
、 的比例计入总评成绩,则该生数学科总评成绩是
的比例计入总评成绩,则该生数学科总评成绩是
分;
(11·佛山)如图物体从点A出发,按照A→B(第1步)→C(第2)→D→A
→E→F→G→A→B→……的顺序循环运动,则第2011步到达点
处;
(11·佛山)如图,D是△ABC的边AB上一点,连 结CD,若AD=2,BD=4,
结CD,若AD=2,BD=4,
∠ACD=∠B,求AC的长;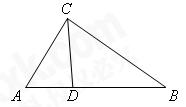
(11·佛山)某市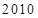 年的用电情况如下图1:
年的用电情况如下图1: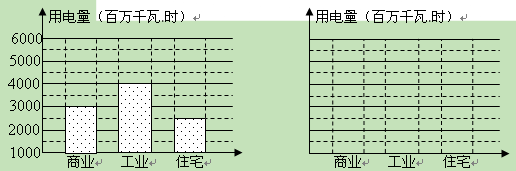
(1)求商业用电量与工业用电量之比是多少?
(2)请在图2上作出更加直观、清楚反映用电比例情况的条形图;
(11·佛山)如图,已知二次函数y=ax2+bx+c的图像经过A(-1,-1)、B(0,2)、C(1,3);
(1)求二次函数的解析式;
( 2)画出二次函数的图像;
2)画出二次函数的图像;
(11·佛山)如图,一张纸上有线段AB;
(1)请用尺规作图,作出线段AB的垂直平分线(保留作图痕迹,不写作法和证明);
(2)若不用尺规作图,你还有其它作法吗?请说明作法(不作图);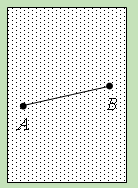
(11·佛山)现在初中课本里所学习的概率计算问题只有以下类型:
第一类是可以列举有限个等可能发生的结果的概率计算问题(一步试验直接列举,两步以上的试验可以借助树状图或表格列举),比如掷一枚均匀硬币的试验;
第二类是用试验或者模拟试验的数据计算频率,并用频率估计概率的概率计算问题,比如掷图钉的试验;
解决概率计算问题,可以直接利用模型,也可以转化后再利用模型;
请解决以下问题
(1)如图,类似课本的一个寻宝游戏,若宝物随机藏在某一块砖下(图中每一块砖除颜色外完全相同),则宝物藏在阴影砖下的概率是多少 ?
?
(2)在 中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
请你根据表中数据,估计构成钝角三角形的概率是多少?(精确到百分位)
(11·佛山)商场对某种商品进行市场调查,1至6月份该种商品的销售情况如下:
①销售成本p(元/千克)与销售月份x的关系如图所示:
③销售量m(千克)与销售月份x满足m=100x+20 0;
0;
试解决以下问题:
(1) 根据图形,求p与x之间的函数关系式;
(2) 求该种商品每月的销售利润y(元)与销售月份x的函数关系式,并求出哪个月的
销售利润最大?
(11·佛山)阅读材料
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;
比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩形、等腰梯形等)来逐步认识四边形;
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=CD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明;
在平面直角坐标系中,下面的点在第一象限的是
| A. | (1,2) | B. | (-2,3) | C. | (0,0) | D. | (-3,-2) |
因式分解x2y-4y的正确结果是
| A.y(x+2)(x-2) | B.y(x+4)(x-4) |
| C.y(x2-4) | D.y(x-2)2 |
如图1,直线EO⊥CD,垂足为点O,AB平分∠EOD,
则∠BOD的度数为
| A.120° | B.130° | C.135° | D.140° |

如图是从一幅扑克牌中取出的两组牌,分别是黑桃1,2,3,4红桃1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌面数字之和等于7的概率是
A. |
B. |
C. |
D. |

如图,在平面直角坐标系中,直线
与矩形
的边
、
分别交于点
、
,已知
,
,则
的面积是

(A)6 (B)3 (C)12 (D)
2011年5月22日—29日在美丽的青岛市举行了苏
迪曼杯羽毛球混合团体锦标赛.在比赛中,某次羽毛球的运动路线可以看作是抛物线 的一部分(如图5),其中出球点B离地面O点的距离是1m,球落地
的一部分(如图5),其中出球点B离地面O点的距离是1m,球落地
点A到O点的距离是4m,那么这条抛物线的解析式是

如图6,点B、C、E在同一条直线上,△ABC与△
CDE都是等边三角形,则下列结论不一定成立的是
(A)△ACE≌△BCD (B)△BGC≌△AFC
(C)△DCG≌△ECF (D)△ADB≌△CEA
图9是由两个长方体组合而成的一个立体图形的三
视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的表面积是________mm2.
如下图,在平面直角坐标系中,对△ABC进行循环
往复的轴对称或中心对称变换,若原来点A坐标是(a,b),则经过第2011次变换后所得
的A点坐标是________.
已知B(2,n)是正比例函数y=2x图象上的点.
(1)求点B的坐标;
(2)若某个反比例函数图象经过点B,求这个反比例函数的解析式.
在今年法国网球公开赛中,我国选手李娜在决赛中
成功击败对手夺冠,称为获得法国网球公开赛冠军的亚洲第一人.某班体育委员就本班同学
对该届法国网球公开赛的了解程度进行全面调查统计,收集数据后绘制了两幅不完整的统计
图,如图(1)和图(2).根据图中的信息,解答下列问题:
(1)该班共有________名学生;
(2)在图(1)中,“很了解”所对应的圆心角的度数为_________;
(3)把图(2)中的条形图形补充完整.
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察
由于受金融危机的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为8万元,今年销售额只有6万元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)若乙型号手机的售价为1400元,为了促销,公司决定每售出一台乙型号手机,返还顾客现金a元,而甲型号手机仍按今年的售价销售,要使(2)中所有方案获利相同,a应取何值?
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C.延长AB交CD于点E.连接AC,作∠DAC=∠ACD,作AF⊥ED于点F,交⊙O于点G.
(1)求证:AD是⊙O的切线;
(2)如 果⊙O的半径是6cm,EC=8cm,求GF的长.
果⊙O的半径是6cm,EC=8cm,求GF的长.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6cm,AB=8cm,BC=14cm.动点P、Q都从点C出发,点P沿C→B方向做匀速运动,点Q沿C→D→A方向做匀速运动,当P、Q其中一点到达终点时,另一点也随之停止运动.
(1)求CD的长;
(2)若点P以1cm/s速度运动,点Q以 cm/s的速度运动,连接BQ、PQ,设△BQP面积为S(cm2),点P、Q运动的时间为t(s),求S与t的函数关系式,并写出t的取
cm/s的速度运动,连接BQ、PQ,设△BQP面积为S(cm2),点P、Q运动的时间为t(s),求S与t的函数关系式,并写出t的取 值范围;
值范围;
(3)若点P的速度仍是1cm/s,点Q的速度为acm/s,要使在运动过程中出现PQ∥DC,请你直接写出a的取值范围.






 的值为( )
的值为( )






 粤公网安备 44130202000953号
粤公网安备 44130202000953号