初中数学一次函数的最值选择题

一次函数y=5x+2的图象不经过的象限是（ ）

A．第一象限

B．第二象限

C．第三象限

D．第四象限

已知正比例函数y=kx（k≠0）的函数值y随x的增大而减小，则一次函数y=x+k的图象大致是（ ）

A．

B．

C．

D．

一次函数y=x-2不经过(   )

A．第一象限

B．第二象限

C．第三象限

D．第四象限

若一次函数y=ax+b（a≠0）的图象与x轴的交点坐标为（﹣2，0），则抛物线y=ax²+bx的对称轴为（ ）

A．直线x=1

B．直线x=﹣2

C．直线x=﹣1

D．直线x=﹣4

如图，已知一次函数y=kx+b的图象，则下列判断中不正确的是（   ）

A．k＞0，b＜0	B．方程kx+b=0的解是x=-3
C．当x＜-3时，y＜0	D．y随x的增大而增大

如果点P在直线y=x+1上，则点P的坐标可以是（）

A．（1，1）

B．（1，0）

C．（2，0）

D．（1，2）

正比例函数y=kx（k≠0）的函数值y随x的增大而减小，则一次函数y=kx+k的图象大致是（ ）

对于一次函数y=x+6，下列结论错误的是（    ）

A．函数值随自变量增大而增大

B．函数图象与x轴正方向成45°角

C．函数图象不经过第四象限

D．函数图象与x轴交点坐标是（0，6）

一次函数y=kx+b（k≠0）的图象如图所示，当y＞0时，x的取值范围是（    ）

A．x＜0

B．x＞0

C．x＜2

D．x＞2

如果函数y=4x与y=的图象的一个交点坐标为（，2），那么另一个交点的坐标为        ．

甲乙两同学从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s（千米）和行驶时间t（时）之间的函数关系的图象，如图所示．根据图中提供的信息，有下列说法：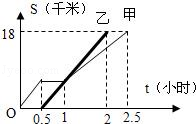

①他们都行驶了18千米．
②甲车停留了0.5小时．
③乙比甲晚出发了0.5小时．
④相遇后甲的速度＜乙的速度．
⑤甲、乙两人同时到达目的地．
其中符合图象描述的说法有（）

A．2个

B．3个

C．4个

D．5个

已知点（﹣4，y₁），（2，y₂）都在直线y=﹣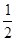x+2上，则y₁，y₂大小关系是（）

A．y1＞y2

B．y1=y2

C．y1＜y2

D．不能比较

下面哪个点在函数y=x+1的图象上（ ）

A．（2，1）

B．（﹣2，1）

C．（2，0）

D．（﹣2，0）

直线y=2x﹣1沿y轴向下平移3个单位，则平移后直线与x轴的交点坐标为（ ）

A．（﹣2，0）

B．（2，0）

C．（4，0）

D．（﹣1，0）

某天早上王文上学，先步行一段路，因时间紧，他又改乘出租车，结果到校时还是迟到了5分钟，其行程情况如图，若他出门时直接乘出租车（车速不变），则他（   ）

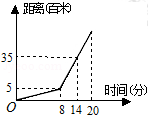
A．仍会迟到2分钟到校	B．刚好按时到校
C．可以提前2分钟到校	D．可以提前5分钟到校