如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图象是( )
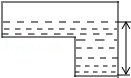
A.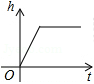 |
B.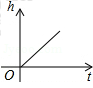 |
C.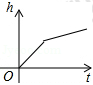 |
D.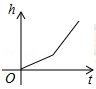 |
下列函数是一次函数的是( )
| A.y=﹣8x | B.y=﹣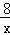 |
C.y=﹣8x2+2 | D.y=﹣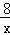 +2 +2 |
如图所示,AB是半圆O的直径,点P从点A出发,沿A→B→O→A的路径运动一周.设OP为s,运动时间为t,则下列图形能大致地刻画s与t之间关系的是()
A. |
B. |
C. |
D. |
一次函数y=kx+k(k<0)的图象大致是( )
A. |
B. |
C. |
D. |
直线y=kx+2过点(1,﹣2),则k的值是( )
| A.4 | B.﹣4 | C.﹣8 | D.8 |
直线y=2x﹣1一定经过点( )
| A.(1,0) | B.(1,2) | C.(0,2) | D.(0,﹣1) |
一次函数y=﹣2x+4的图象与y轴的交点坐标是( )
| A.(0,4) | B.(4,0) | C.(2,0) | D.(0,2) |
一次函数y=﹣2x+3的图象不经过的象限是( )
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
点(1,m),(2,n)在函数y=-x+1的图象上,则m、n的大小关系是( )
| A.m>n | B.m<n | C.m=n | D.m≤n |
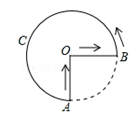
世界文化遗产“华安二宜楼”是一座圆形的土楼,如图,小王从南门点A沿AO匀速直达土楼中心古井点O处,停留拍照后,从点O沿OB也匀速走到点B,紧接着沿 回到南门,下面可以近似地刻画小王与土楼中心O的距离s随时间t变化的图象是( )
回到南门,下面可以近似地刻画小王与土楼中心O的距离s随时间t变化的图象是( )
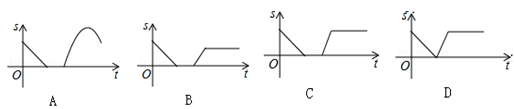
一次函数y=(m+2)x+(1+m)的图象如图所示,则m的取值范围是( )

| A.m>﹣1 | B.m<﹣2 | C.﹣2<m<﹣1 | D.m<﹣1 |
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:
①快递车从甲地到乙地的速度为100千米/时;
②甲、乙两地之间的距离为120千米;
③快递车由原路返回时,经过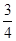 小时与货车相遇;
小时与货车相遇;
④图中点B的坐标为(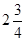 ,75);
,75);
⑤快递车从乙地返回时的速度为90千米/时;以上5个结论中正确有( )个.
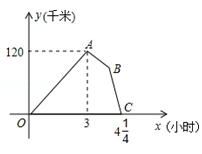
| A.2个 | B.3个 | C.4个 | D.5个 |
设min{x,y}表示x,y两个数中的最小值,例如min{1,2}=1,min{7,5}=5,则关于x的一次函数y=min{2x,x+1}可以表示为( )
| A.y="2x" | B.y=x+1 |
C. |
D.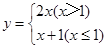 |
在下列函数中,y随x增大而增大的是( )
A. |
B. |
C.y=x﹣3 | D.y=x2+3 |
下列函数中,是正比例函数的是( )
| A.y=﹣8x | B.y= |
C.y=5x2+6 | D.y=﹣0.5x﹣1 |