初中数学一次函数的最值试题

如图1所示，某乘客乘高速列车从甲地经过乙地到丙地，列车匀速行驶，图2为列车离乙地路程y（千米）与行驶时间x（小时）时间的函数关系图象． 
（1）填空：甲、丙两地距离         千米． 
（2）求高速列车离乙地的路程y与行驶时间x之间的函数关系式，并写出x的取值范围．

为了能有效地使用电力资源，跃进花园小区实行居民峰谷用电，居民家庭在峰时段（上午8：00—晚上21：00）用电的电价为0．55元/度，谷时段（晚上21：00—次日晨8：00）用电的电价为0．35元/度．
（1）若朱老师家某月用电100度，其中峰时段用电度，这个月应缴纳电费      度；当朱老师家峰时段用电60度时，求应缴纳电费．
（2）朱老师生活节俭，每天早晨5：30起身后立即用额定功率1500瓦的电水壶烧水，10分钟能烧开一壶水。问朱老师家一年内用电水壶烧水共耗电多少度？能节省电费多少元？（一年按实际烧水360天计算，1度=1千瓦．时）

在直角坐标系中，等腰直角三角形A₁B₁O、A₂B₂B₁、A₃B₃B₂、…、A_nB_nB_n－1按如图所示的方式放置，其中点A₁、A₂、A₃、…、A_n均在一次函数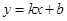的图像上，点B₁、B₂、B₃、…、B_n均在x轴上。若点B₁的坐标为（1，0），点B₂的坐标为（3，0），则点A_n的坐标为（   ）

A．（，）	B．（，）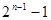
C．（，+1）	D．（，）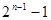

学校需要到印刷厂印刷x份材料，甲印刷厂提出：每份材料收0.2元印刷费，另收500元制版费；乙印刷厂提出：每份材料收0.4元印刷费，不收制版费．
（1）两印刷厂的收费各是多少元？（用含x的代数式表示）
（2）学校要印刷2400份材料，若不考虑其他因素，选择哪家印刷厂比较合算？试说明理由．

某空调器销售商，今年四月份销出空调（a﹣1）台，五月份销售空调比四月份的2倍少1台，六月份销售空调比前两个月的总和的4倍还多5台．
（1）用代数式表示该销售商今年第二季度共销售空调多少台？
（2）若a=220，求第二季度销售的空调总数．

如图，在△ABC中，∠BAC=90°，AB=AC=6，D为BC的中点．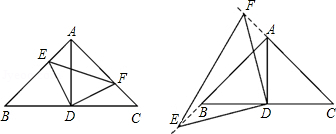

（1）若E、F分别是AB、AC上的点，且AE=CF，求证：△AED≌△CFD；
（2）当点F、E分别从C、A两点同时出发，以每秒1个单位长度的速度沿CA、AB运动，到点A、B时停止；设△DEF的面积为y，F点运动的时间为x，求y与x的函数关系式；
（3）在（2）的条件下，点F、E分别沿CA、AB的延长线继续运动，求此时y与x的函数关系式．

如图1，已知：抛物线y=x²+bx+c与x轴交于A，B两点，与y轴交于点C，经过B，C两点的直线是y=x-2，连结AC．

（1）求出抛物线的函数关系式；
（2）若△ABC内部能否截出面积最大的矩形DEFC（顶点D、E、F、G在△ABC各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由．
（3）点P（t，0）是x轴上一动点，P、Q两点关于直线BC成轴对称，PQ交BC于点M，作QH⊥x轴于点H．连结OQ，是否存在t的值，使△OQH与△APM相似？若存在，求出t的值；若不存在，说明理由．

某零件制造车间有工人20名，已知每名工人每天可制造甲种零件6个或乙种零件5个，且每制造一个甲种零件，可获利润150元，每制造一个乙种零件可获利润260元，在这20名工人中，车间每天安排x名工人制造甲种零件，其余工人制造乙种零件，且生产乙种零件的个数不超过甲种零件个数的一半．
（1）请写出此车间每天所获利润y（元）与x（人）之间的函数关系式；
（2）求自变量x的取值范围；
（3）怎样安排生产，每天获得的利润最大，最大利润是多少？

如图，在平面直角坐标系中，直线y=﹣x+交直线y=kx（k＞0）于点B，平行于y轴的直线x=7交它们于点A、C，且AC=15．

（1）求∠OBC的度数；
（2）若正方形的四个顶点恰好在射线AB、射线CB及线段AC上，请直接写出射线AB上的正方形顶点的坐标．（不需要写出计算过程）．

A市和B市分别有某种库存机器12台和6台，现决定支援C村10台，D村8台，已知从A市调运一台机器到C村和D村的运费分别是400元和800元，从B市调运一台机器到C村和D村的运费分别是300元和500元．
（1）设B市运往C村机器x台，求总运费W关于x的函数关系式；
（2）若要求总运费不超过9000元，共有几种调运方案？
（3）求出总运费最低的调运方案，最低运费是多少元？
分析由已知条件填出下表：

库存机器	支援C村	支援D村
B市6台	x台	（6﹣x）台
A市12台	（10﹣x）台	[8﹣（6﹣x）]台

 

如图，直线y=﹣x+1交y轴于A点，交x轴于C点，以A，O，C为顶点作矩形AOCB，将矩形AOCB绕O点逆时针旋转90°，得到矩形DOFE，直线AC交直线DF于G点．

（1）求直线DF的解析式；
（2）求证：OG平分∠CGD；
（3）在第一象限内，是否存在点H，使以G，O，H为顶点的三角形为等腰直角三角形？若存在请求出点H的坐标；若不存在，请什么理由．

为庆祝商都正式营业，商都推出了两种购物方案．方案一：非会员购物所有商品价格可获九五折优惠，方案二：如交纳300元会费成为该商都会员，则所有商品价格可获九折优惠．
（1）以x（元）表示商品价格，y（元）表示支出金额，分别写出两种购物方案中y关于x的函数解析式；
（2）若某人计划在商都购买价格为5880元的电视机一台，请分析选择哪种方案更省钱？

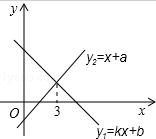
一次函数y₁=kx+b与y₂=x+a的图象如图，则下列结论：①k＜0；②a＞0：③b＞0；④x＜2时，kx+b＜x+a中，正确的个数是（ ）

A．1

B．2

C．3

D．4

【问题情境】
张老师给爱好学习的小林和小兰提出这样一个问题：如图①，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．

小林的证明思路是：如图②，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．
小兰的证明思路是：如图②，过点P作PG⊥CF，垂足为G，通过证明四边形PDFG是矩形，
可得：PD=GF，PE=CG，则PD+PE=CF．
【变式探究】如图③，当点P在BC延长线上时，其余条件不变，求证：PD﹣PE=CF；
【结论运用】请运用上述解答中所积累的经验和方法完成下列两题：
如图④，在平面直角坐标系中有两条直线l₁：y=x+3、l₂：y=﹣3x+3，若l₂上的一点M到l₁的距离是1，请运用上述的结论求出点M的坐标．

某公司生产的一种时令商品每件成本为20元，经过市场调研发现，这种商品在未来20天内的日销售量m（件）与时间t（天）的关系如表：

时间t（天）	1	3	6	10	…
日销售量m（件）	94	90	84	76	…

 
未来20天内每天的价格y（元/件）与时间t（天）的函数关系式为y=t+25（1≤t≤20且t为整数）．
（1）认真分析表中的数据，用所学过的函数知识，确定一个满足这些数据的m（件）与t（天）之间的关系式；
（2）设未来20天日销售利润为p（元）．请求出p（元）与t（天）之间的关系式；并预测未来20天中哪一天的日销售利润最大，最大日销售利润是多少？