江苏省张家港梁丰初中八年级上学期期中考试数学试卷
在-0.101001, ,
, ,-
,- ,0中,无理数的个数是 ( )
,0中,无理数的个数是 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
某市参加中考的学生人数约为6.01×104人.对于这个近似数,下列说法正确的是( )
| A.精确到百分位 | B.精确到百位 | C.精确到十位 | D.精确到个位 |
下列四组线段中,可以构成直角三角形的是 ( )
| A.1.5,2,2.5 | B.4,5,6 | C.2,3,4 | D.1, ,3 ,3 |
如果 在实数范围内有意义,那么x的取值范围是( )
在实数范围内有意义,那么x的取值范围是( )
A.x ≠- |
B.x<- |
C.x≥- |
D. ≥ ≥ |
与点P( )在同一个象限内的点是( )
)在同一个象限内的点是( )
| A.(3,2) | B.(—3,2) | C.(—3,2) | D.(3,—2) |
设边长为3的正方形的对角线长为 .下列关于
.下列关于 的四种说法:①
的四种说法:① 是无理数;②
是无理数;② 可以用数轴上的一个点来表示;③3<
可以用数轴上的一个点来表示;③3< <4;④
<4;④ 是18的算术平方根.其中,所有正确说法的序号是( )
是18的算术平方根.其中,所有正确说法的序号是( )
| A.①④ | B.②③ | C.①②④ | D.①③④; |
如图所示是我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形拼成的大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b, 那么(a+b)2的值是( )

| A.169 | B.25 | C.19 | D.13 |
若A(x1,y1)、B(x2,y2)是一次函数y=(a﹣2)x+1图象上的不同的两个点,当x1>x2时,y1<y2,则a的取值范围是( )
| A.a<0 | B.a>0 | C.a<2 | D.a>2 |
在直角坐标系中,等腰直角三角形A1B1O、A2B2B1、A3B3B2、…、AnBnBn-1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数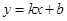 的图像上,点B1、B2、B3、…、Bn均在x轴上。若点B1的坐标为(1,0),点B2的坐标为(3,0),则点An的坐标为( )
的图像上,点B1、B2、B3、…、Bn均在x轴上。若点B1的坐标为(1,0),点B2的坐标为(3,0),则点An的坐标为( )

A.( , , ) ) |
B.( , ,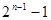 ) ) |
C.( , , +1) +1) |
D.(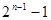 , , ) ) |
已知一直角三角形的两直角边的长分别为6和8,则斜边上中线的长度是____ __.
已知点A(x,1)与点B(2,y)关于原点对称,则(x-y)2013的值为____ ___.
有下列说法:①无限小数是无理数;②5的平方根是 ;③8的立方根是
;③8的立方根是 ;④使代数式
;④使代数式 有意义的
有意义的 取值范围是
取值范围是 ;⑤与数轴上的点一一对应的点是有理数.其中正确的是 (只需要填写序号).
;⑤与数轴上的点一一对应的点是有理数.其中正确的是 (只需要填写序号).
如图,A、B的坐标分别为(1,0)、(0,2),若将线段AB平移到至 ,
, 、
、 的坐标分别为
的坐标分别为 、
、 ,则
,则 = .
= .

如图,在Rt△ABC中,∠C=90°,∠ABC=60°,点D是BC边上的点,BD=2,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是_______.
(本题6分)在△ABC中,AB、BC、AC三边的长分别为 、
、 、
、 ,
,
(1)请在正方形网格中画出格点△ABC;
(2)求出这个三角形ABC的面积.

(本题8分)已知一次函数y=kx+b的图象经过点A(—1,—5),且与正比例函数 的图象相交于点B(2,a).
的图象相交于点B(2,a).
(1)求a的值;
(2)求一次函数y=kx+b的表达式;
(3)在同一坐标系中,画出这两个函数的图象,并求这两条直线与y轴围成的三角形的面积.
(本题6分)已知点P(m,n)在第一象限,并且在一次函数y=2x-1的图像上,求实数m的取值范围.
如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
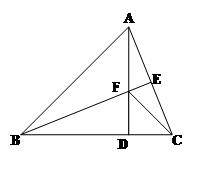
(1)求证:BF=2AE;
(2)若CD=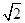 ,求AD的长.
,求AD的长.
(本题8分)为了发展旅游经济,我市某景区采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票金额为y1(元),节假日购票金额为y2(元).y1、y2与x之间的函数关系如图所示.
(1)观察图象可知:a=_______;b=_______;m=_______.
(2)直接写出y1、y2与x之间的函数关系式.
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A、B两个团队合计50人,A、B两个团队各有多少人?
(本题10分)如图,在平面直角坐标系中,直线 +2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
(1)求点A、B的坐标,并求边AB的长;
(2)求点D和点C的坐标;
(3)你能否在x轴上找一点M,使△MDB的周长最小?如果能,请求出M点的坐标;如果不能,说明理由.

 的平方根是 .
的平方根是 . 和
和 的图像相交于点
的图像相交于点 ,则关于
,则关于 的不等式
的不等式 的解集为______ _____.
的解集为______ _____.


 的值:(本题每小题4分,共8分)
的值:(本题每小题4分,共8分) ;
;  ;
;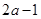 的平方根是
的平方根是 ,
, 的立方根是2,
的立方根是2, 是
是 的整数部分,求
的整数部分,求 的平方根.
的平方根.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号