初中数学二次函数在给定区间上的最值填空题

一个足球从地面上被踢出，它距地面高度y（米）可以用二次函数y=－4．9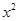+19．6x刻画，其中x（秒）表示足球被踢出后经过的时间．则足球被踢出后到离开地面达到最高点所用的时间是        秒．

二次函数y=x²的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数y=x²的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积是______．

抛物线与轴的交点坐标是          ．

三张完全相同的卡片上分别写有函数，，，从中随机抽取一张，则所得卡片上函数的图象在第一象限内随的增大而增大的概率是      ．

将抛物线的图象向右平移3个单位，再向上平移4个单位后，得到的新抛物线解析式是        ．

在函数中，若，那么函数的最大值是      ．

一小球被抛出后，距离地面的高度h（m）和飞行时间t（s） 满足函数关系式为，则小球距离地面的最大高度是         m．

如图，二次函数y=ax²+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于点C，点B坐标是（﹣1，0），对称轴为直线x=1，下面的四个结论：  

①9a+3b+c=0；②a+b＞0；③ac＞0；④b²﹣4ac＞0．其中正确的结论序号是          ．

已知抛物线与轴交于点A，点B，与轴交于点C，若D为AB的中点，则
CD的长为            ．

已知k，n均为非负实数，且2k+n=2，则代数式2k²﹣4n的最小值为              ．

如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线与扇形OAB的边界总有两个公共点，则实数k的取值范围是____________．

已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如表：

x	…	﹣1	0	1	2	3	…
y	…	10	5	2	1	2	…

 
则当y＜5时，x的取值范围是        ．

如图所示的二次函数y=ax²+bx+c的图象中，刘星同学观察得出了下面四条信息：①b²-4ac＞0；②c＞1；③2a－b＜0；④a+b+c＜0．你认为其中正确的有________．（填序号）

将二次函数y=3（x+2）²-4的图象向右平移3个单位，再向上平移1个单位，所得的图象的函数关系式为                ．

如图，二次函数的图象与x轴相交于点（﹣1，0）和（3，0），则它的对称轴是_________．