黄冈市与A市之间的城际铁路正在紧张有序地建设中.在建成通车前,进行了社会需
求调查,得到一列火车一天往返次数m与该列车每次拖挂车厢节数n的部分数据如下:
| 车厢节数n |
4 |
7 |
10 |
| 往返次数m |
16 |
10 |
4 |
(1)请你根据上表数据,在三个函数模型:①y=kx+b(k、b为常数,k≠0);②y= (k为常数,k≠0);③y=ax2+bx+c(a、b、c为常数,a≠0)中,选取一个适合的函数模型,求出的m关于n的函数关系式是m= (不写n的取值范围)
(k为常数,k≠0);③y=ax2+bx+c(a、b、c为常数,a≠0)中,选取一个适合的函数模型,求出的m关于n的函数关系式是m= (不写n的取值范围)
(2)结合你求出的函数,探究一列火车每次挂多少节车厢,一天往返多少次时,一天的设计运营人数Q最多(每节车厢载客量设定为常数p).
如图,抛物线 :
: ,将该抛物线向左并向上平移,使顶点Q的对应点是Q′,抛物线
,将该抛物线向左并向上平移,使顶点Q的对应点是Q′,抛物线 与
与 轴的右交点P的对应点是P′,点P′、Q′都在坐标轴上,则在这个平移的过程中,抛物线
轴的右交点P的对应点是P′,点P′、Q′都在坐标轴上,则在这个平移的过程中,抛物线 上曲线段PQ扫过的面积(即图中阴影部分的面积)为 .
上曲线段PQ扫过的面积(即图中阴影部分的面积)为 .
已知抛物线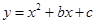 的对称轴为
的对称轴为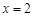 ,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为 .
,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为 .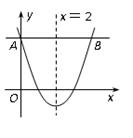
将抛物线的解析式y= 向上平移3个单位长度,在向右平移1个单位长度后,得到的抛物线的解析式是 .
向上平移3个单位长度,在向右平移1个单位长度后,得到的抛物线的解析式是 .
已知函数y=k -2x-k-2的图象与坐标轴有两个交点,则k的值为 .
-2x-k-2的图象与坐标轴有两个交点,则k的值为 .
二次函数y=a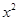 +bx+c(a≠0)的图象如图,若
+bx+c(a≠0)的图象如图,若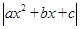 =k(k≠0)有两个不相等的实数根,则k的取值范围是 .
=k(k≠0)有两个不相等的实数根,则k的取值范围是 .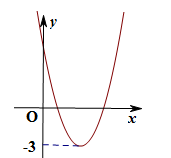
二次函数y = x2-2x-2的图象在坐标平面内绕顶点旋转180°,再向左平移3个单位,向上平移5个单位后图象对应的二次函数解析式为___________.
如图,抛物线y =- x2+bx+ c过A(0,2),B(1,3),CB⊥x轴于点C,四边形CDEF为正方形,点D在线段BC上,点E在此抛物线上,且在直线BC的左侧,则正方形CDEF的边长为 .
x2+bx+ c过A(0,2),B(1,3),CB⊥x轴于点C,四边形CDEF为正方形,点D在线段BC上,点E在此抛物线上,且在直线BC的左侧,则正方形CDEF的边长为 .
二次函数y =mx2+(m+2)x+ m+2的图象与x轴只有一个交点,那么m的值为 .
m+2的图象与x轴只有一个交点,那么m的值为 .
将二次函数 的图象沿x轴向左平移2个单位,则平移后的抛物线对应的二次函数的表达式为 .
的图象沿x轴向左平移2个单位,则平移后的抛物线对应的二次函数的表达式为 .
在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若 ,则称点Q为点P的“可控变点”.
,则称点Q为点P的“可控变点”.
例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)若点(﹣1,﹣2)是一次函数 图象上点M的“可控变点”,则点M的坐标为 ;
图象上点M的“可控变点”,则点M的坐标为 ;
(2)若点P在函数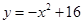 (
(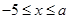 )的图象上,其“可控变点”Q的纵坐标y′的取值范围是
)的图象上,其“可控变点”Q的纵坐标y′的取值范围是 ,则实数a的取值范围是 .
,则实数a的取值范围是 .
如果将抛物线 向上平移,使它经过点
向上平移,使它经过点 ,那么所得新抛物线的表达式是_______________.
,那么所得新抛物线的表达式是_______________.
二次函数 的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数
的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数 的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
已知点A(4,y1),B( ,y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .
,y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .