初中数学二次函数在给定区间上的最值解答题

如图，在直角梯形ABCD中，∠D=∠BCD=90°，∠B=60°，AB = 6，AD = 9，点E是CD上的一个动点（E不与D重合），过点E作EF∥AC，交AD于点F（当E运动到C时，EF与AC重合），把△DEF沿着EF对折，点D的对应点是点G,如图①．

⑴ 求CD的长及∠1的度数；
⑵ 设DE = x，△GEF与梯形ABCD重叠部分的面积为y．求y与x之间的函数关系式，并求x为何值时，y的值最大?最大值是多少?
⑶ 当点G刚好落在线段BC上时,如图②,若此时将所得到的△EFG沿直线CB向左平移，速度为每秒1个单位，当E点移动到线段AB上时运动停止.设平移时间为t（秒）,在平移过程中是否存在某一时刻t，使得△ABE为等腰三角形?若存在，请直接写出对应的t的值；若不存在，请说明理由.

在如图的直角坐标系中，已知点A(2,0)、B(0，－4)，将线段AB绕点A按逆时针方向旋转90°至AC．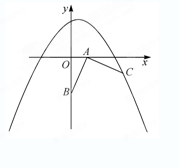

(1)求点C的坐标；
(2)若抛物线y＝－x²＋ax＋4经过点C．
①求抛物线的解析式；
②在抛物线上是否存在点P(点C除外)使△ABP是以AB为直角边的等腰直角三角形?若存在，求出所有点P的坐标；若不存在，请说明理由．

如图，抛物线y=－x+4x+5交x轴于A、B（以A左B右)两点，交y轴于点C.

(1)求直线BC的解析式；
(2)点P为抛物线第一象限函数图象上一点，设P点的横坐标为m，△PBC的面积为S，求S与m的函数关系式；
(3)在(2)的条件下，连接AP，抛物线上是否存在这样的点P，使得线段PA被BC平分，如果不存在，请说明理由；如果存在，求点P的坐标.

如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点D、E、F分别是边AB，BC，AC的中点，连接DE，DF，动点P，Q分别从点A、B同时出发，运动速度均为1cm/s，点P沿AFD的方向运动到点D停止；点Q沿BC的方向运动，当点P停止运动时，点Q也停止运动．在运动过程中，过点Q作BC的垂线交AB于点M，以点P，M，Q为顶点作平行四边形PMQN．设平行四边形边形PMQN与矩形FDEC重叠部分的面积为y（cm²）（这里规定线段是面积为0有几何图形），点P运动的时间为x（s）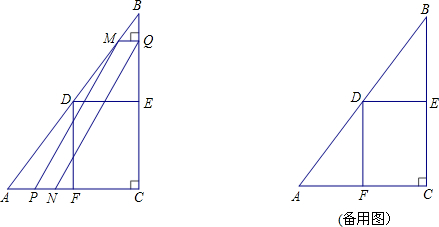

（1）当点P运动到点F时，CQ=          cm；
（2）在点P从点F运动到点D的过程中，某一时刻，点P落在MQ上，求此时BQ的长度；
（3）当点P在线段FD上运动时，求y与x之间的函数关系式．

已知：如图①，在平行四边形ABCD中，AB=12，BC=6，AD⊥BD．以AD为斜边在平行四边形ABCD的内部作Rt△AED，∠EAD=30°，∠AED=90°．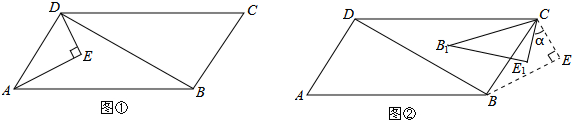

（1）求△AED的周长；
（2）若△AED以每秒2个单位长度的速度沿DC向右平行移动，得到△A₀E₀D₀，当A₀D₀与BC重合时停止移动，设运动时间为t秒，△A₀E₀D₀与△BDC重叠的面积为S，请直接写出S与t之间的函数关系式，并写出t的取值范围；
（3）如图②，在（2）中，当△AED停止移动后得到△BEC，将△BEC绕点C按顺时针方向旋转α（0°＜α＜180°），在旋转过程中，B的对应点为B₁，E的对应点为E₁，设直线B₁E₁与直线BE交于点P、与直线CB交于点Q．是否存在这样的α，使△BPQ为等腰三角形？若存在，求出α的度数；若不存在，请说明理由．

如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，抛物线y=-x²+bx+c经过A、B两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D．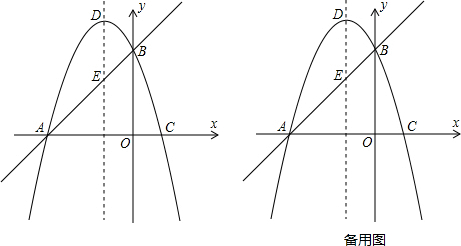

（1）求抛物线的解析式；
（2）在第三象限内，F为抛物线上一点，以A、E、F为顶点的三角形面积为3，求点F的坐标；
（3）点P从点D出发，沿对称轴向下以每秒1个单位长度的速度匀速运动，设运动的时间为t秒，当t为何值时，以P、B、C为顶点的三角形是直角三角形？直接写出所有符合条件的t值．

如图，已知直线y＝－2x＋4与x轴、y轴分别相交于A、C两点，抛物线y=-2x²+bx+c (a≠0)经过点A、C.

（1）求抛物线的解析式;
（2）设抛物线的顶点为P，在抛物线上存在点Q，使△ABQ的面积等于△APC面积的4倍.求出点Q的坐标;
（3）点M是直线y=-2x+4上的动点，过点M作ME垂直x轴于点E，在y轴（原点除外）上是否存在点F，使△MEF为等腰直角三角形? 若存在,求出点F的坐标及对应的点M的坐标；若不存在，请说明理由.

如图，在平面直角坐标系中，二次函数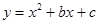的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为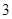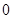（，），与y轴交于C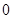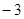（，）点，点P是直线BC下方的抛物线上一动点.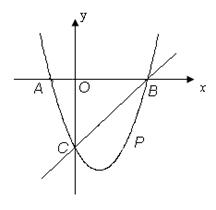

（1）求这个二次函数的表达式．
（2）连结PO、PC，并把△POC沿CO翻折，得到四边形POP’C，那么是否存在点P，使四边形POP’C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.

如图，直角坐标系中Rt△ABO，其顶点为A(0, 1)、B(2, 0)、O(0, 0)，将此三角板绕原点O逆时针旋转90°，得到Rt△A′B′O．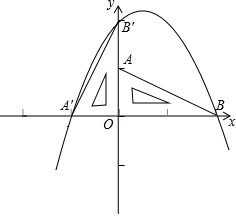

（1）一抛物线经过点A′、B′、B，求该抛物线的解析式；
（2）设点P是在第一象限内抛物线上的一动点，是否存在点P，使四边形PB′A′B的面积是△A′B′O面积4倍？若存在，请求出P的坐标；若不存在，请说明理由．
（3）在（2）的条件下，试指出四边形PB′A′B是哪种形状的四边形？并写出四边形PB′A′B的两条性质．

 已知在平面直角坐标系xoy中，二次函数y=-2x²+bx+c的图像经过点A（-3,0）和点B（0,6）。（1）求此二次函数的解析式；（2）将这个二次函数的图像向右平移5个单位后的顶点设为C，直线BC与x轴相交于点D,求∠sin∠ABD；（3）在第（2）小题的条件下，连接OC，试探究直线AB与OC的位置关系，并且说明理由。

如图，已知抛物线y=x²-1与x轴交于A、B两点，与y轴交于点C．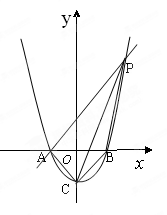

（1）求A、B、C三点的坐标．
（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．
（3）在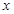轴上方的抛物线上是否存在一点M，过M作MG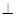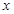轴于点G，使以A、M、G三点为顶点的三角形与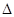PCA相似．若存在，请求出M点的坐标；否则，请说明理由．

如图，在平面直角坐标系xOy中，一次函数y=x+m (m为常数)的图像与x轴交于点A(－3,0)，与y轴交于点C．以直线x=1为对称轴的抛物线y=ax²+bx+c(a，b，c为常数，且a≠0)经过A、C两点，并与x轴的正半轴交于点B．

(1)求m的值及抛物线的函数表达式；
(2)若P是抛物线对称轴上一动点，△ACP周长最小时，求出P的坐标；
(3)是否存在抛物在线一动点Q，使得△ACQ是以AC为直角边的直角三角形？若存在，求出点Q的横坐标；若不存在，请说明理由；
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M₁(x₁,y₁)，M₂(x₂,y₂)两点，试问是否为定值，如果是，请直接写出结果，如果不是请说明理由．

如图，在平面直角坐标系中，二次函数y=x²+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．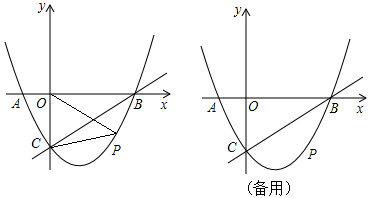

（1）求这个二次函数的表达式．
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．

如图，已知在平面直角坐标系中，四边形ABCO是梯形，且BC∥AO，其中A（6，0），B（3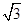，），∠AOC=60°，动点P从点O以每秒2个单位的速度向点A运动，动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动，当点P到达A点时，点Q也随之停止，设点P，Q运动的时间为t（秒）．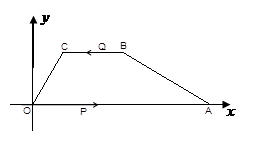

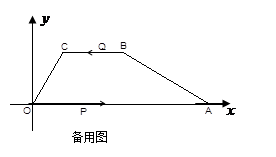
（1）求点C的坐标及梯形ABCO的面积；
（2）当点Q在CO边上运动时，求△OPQ的面积S与运动时间t的函数关系式，并写出自变量t的取值范围；
（3）以O，P，Q为顶点的三角形能构成直角三角形吗？若能，请求出t的值；若不能，请说明理由．

已知直线y=x+6交x轴于点A，交y轴于点C，经过A和原点O的抛物线y=ax²+bx(a＜0）的顶点B在直线AC上.

（1）求抛物线的函数关系式；
（2）以B点为圆心，以AB为半径作⊙B，将⊙B沿x轴翻折得到⊙D，试判断直线AC与⊙D的位置关系，并说明理由；
（3）若E为⊙B优弧上一动点,连结AE、OE，问在抛物线上是否存在一点M，使∠MOA︰∠AEO=2︰3，若存在，试求出点M的坐标；若不存在，试说明理由.