广东汕头澄海区九年级第一学期期末考试数学试卷
小明制作了十张卡片,上面分别标有1~10这十个数字.从这十张卡片中随机抽取一张恰好能被4整除的概率是( )
A. |
B. |
C. |
D. |
如图,DC 是⊙O的直径,弦AB⊥CD于F,连结BC,DB,则下列结论错误的是( )
| A.弧AD=弧BD | B.AF=BF | C.OF=CF | D.∠DBC=90° |
在平面直角坐标系中,线段OP的两个端点坐标分别是O(0,0),P(4,3),将线段OP绕点O逆时针旋转90°到OP′位置,则点P′的坐标为( )
| A.(3,4) | B.(﹣4,3) | C.(﹣3,4) | D.(4,﹣3) |
如果一个三角形的其中两边长分别是方程 的两个根,那么连结这个三角形三边的中点,得到的三角形的周长可能是( )
的两个根,那么连结这个三角形三边的中点,得到的三角形的周长可能是( )
| A.5.5 | B.5 | C.4.5 | D.4 |
把一副三角板如图(1)放置,其中 ,
, ,
, ,斜边
,斜边 ,
, .把三角板
.把三角板 绕着点C顺时针旋转
绕着点C顺时针旋转 得到△
得到△ (如图2),此时AB与
(如图2),此时AB与 交于点O,则线段
交于点O,则线段 的长度为( )
的长度为( )
A. |
B. |
C. |
D.4 |
如图,已知OA,OB是⊙O的两条半径,且OA⊥OB,点C在圆周上(与点A、B不重合),则∠ACB的度数为 .
如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= .
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是 . 
如图,在边长为1个单位长度的小正方形组成的方格中,点A、B、C都是格点.
(1)将△ABC绕点O按逆时针方向旋转180°得到△A1B1C1,请画出△A1B1C1;
(2)依次连结BC1、B1C,猜想四边形BC1B1C是什么特殊四边形?并说明理由.
某校九年级举行毕业典礼,需要从九年(1)班的2名男生1名女生(男生用A1表示,女生用B1表示)和九年(2)班的1名男生1名女生(男生用A2表示,女生用B2表示)共5人中随机选出2名主持人.(1)用树状图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连结AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
某商场今年二月份的营业额为400万元,三月份由于经营不善,其营业额比二月份下降10%.后来通过加强管理,五月份的营业额达到518.4万元.求三月份到五月份营业额的月平均增长率.
已知关于 的一元二次方程
的一元二次方程 .
.
(1)若 是这个方程的一个根,求
是这个方程的一个根,求 的值和它的另一根;
的值和它的另一根;
(2)对于任意的实数 ,判断原方程根的情况,并说明理由.
,判断原方程根的情况,并说明理由.
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF= ,求⊙O的半径r.
,求⊙O的半径r.
如图,已知在平面直角坐标系中,四边形ABCO是梯形,且BC∥AO,其中A(6,0),B(3,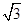 ),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).
),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).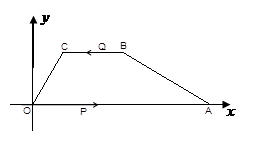
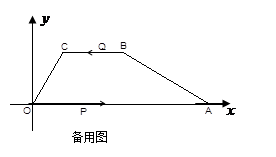
(1)求点C的坐标及梯形ABCO的面积;
(2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围;
(3)以O,P,Q为顶点的三角形能构成直角三角形吗?若能,请求出t的值;若不能,请说明理由.
 的值为( )
的值为( )

 有意义,那么x的取值范围是( )
有意义,那么x的取值范围是( )







 有一个根为2,则另一根为( )
有一个根为2,则另一根为( ) .
. 的根是 .
的根是 . ★
★ =
= ,如:3★5=
,如:3★5= ,若
,若 ★2=6,则实数x的值是 .
★2=6,则实数x的值是 .
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号