江苏省无锡市南长区九年级上学期期末考试数学试卷
已知两圆的半径分别为2和4,圆心距为6,则两圆的位置关系是( )
| A.相交 | B.内切 | C.外切 | D.内含 |
把抛物线y=3x2沿y轴向上平移8个单位,所得抛物线的函数关系式为( )
| A.y=3x2+8 | B.y=3x2-8 | C.y=3(x+8) 2 | D.y=3(x-8) 2 |
如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,下列结论正确的是… ( )
A.sinA= |
B.tanA= |
C.cosB= |
D.tanB= |
二次函数y=x2-(m-1)x+4的图像与x轴有且只有一个交点,则m的值为( )
| A.1或-3 | B.5或-3 | C.-5或3 | D.以上都不对 |
半径为2的圆中,弦AB、AC的长分别2和2 ,则∠BAC的度数是( )
,则∠BAC的度数是( )
A.15° B.15°或45° C.15°或75° D.15°或105°
如图是二次函数y=ax2+bx+c图像的一部分,其对称轴是直线x=-1,且过点(-3,0),下列说法:①abc>0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(2.5,y2)是抛物在线两点,则y1>y2,其中正确的是( )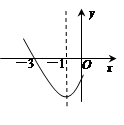
| A.② | B.②③ | C.②④ | D.①② |
某小区今年2月份绿化面积为6400m2,到了今年4月份增长到8100m2,假设绿化面积月平均增长率都相同,则增长率为___________.
如图,在正八边形ABCDEFGH中,四边形BCFG的面积为30cm2,则正八边形的面积为_______ cm2.
如图,等腰△AOB中,∠AOB=120°,AO=BO=2,点C为平面内一点,满足∠ACB=60°,且OC的长度为整数,则所有满足题意的OC长度的可能值为 .
如图,从热气球P上测得两建筑物A、B的底部的俯角分别为45°和30°,如果A、B两建筑物的距离为60米,P点在地面上的正投影恰好落在线段AB上,求热气球P的高度.(结果保留根号)
李大爷几年前承包了甲、乙两片荒山,各栽100棵杨梅树,现已结果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量数如折线统计图所示.
(1)分别计算甲、乙两片山上杨梅产量数样本的平均数;
(2)试通过计算说明,哪片山上的杨梅产量较稳定?
如图,在△ABC中,D、E分别是AB、AC的中点.BE=2DE,延长DE到点F,使得EF=BE,连接CF. 
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留 和根号).
和根号).
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售数量x(千件)的关系为:y1= 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=
(1)用x的代数式表示t,则t=__________;当0<x≤3时,y2与x的函数关系式为:y2=__________________;当3≤x<________时,y2=100;
(2)当3≤x<6时,求每年该公司销售这种健身产品的总利润w(千元)与国内的销售数量x(千件)的函数关系式,并求此时的最大利润.
如图,在平面直角坐标系xOy中,一次函数y= x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)若P是抛物线对称轴上一动点,△ACP周长最小时,求出P的坐标;
(3)是否存在抛物在线一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若不存在,请说明理由;
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=4 ,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC= 度;
(2)如图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,当D在BA的延长线上时,设BF=x,两块三角板重迭部分的面积为y.求y与x的函数关系式,并求出对应的x取值范围.
 有意义的x的取值范围是( )
有意义的x的取值范围是( ) =4
=4 ÷
÷ ·
·
 =±2
=±2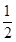 (x-2)2+9的图像的顶点坐标为 .
(x-2)2+9的图像的顶点坐标为 . ,则AB长为____米.
,则AB长为____米.
 -(3-π)0-
-(3-π)0-
 )(1-
)(1-
 粤公网安备 44130202000953号
粤公网安备 44130202000953号