如图1,在平面直角坐标系中,正方形OABC的顶点A和C分别在x轴和y轴正半轴上,点B坐标为(3,3),抛物线y=﹣x2+bx+c过点A、C,交x轴负半轴于点D,与BC边的另一个交点为E,抛物线的顶点为M,对称轴交x轴于点N.
(1)求抛物线的函数关系式;
(2)点P在直线MN上,求当PE+PA的值最小时点P的坐标;
(3)如图2,探索在x轴是否存在一点F,使∠CFO=∠CDO﹣∠CAO?若存在,求点F的坐标;不存在,说明理由;
(4)将抛物线沿y轴方向平移m个单位后,顶点为Q,若QO平分∠CQN,求点Q的坐标.
如图,抛物线y=x2+bx+c的顶点为D(﹣1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A,B两点(点A在点B的左侧).
(1)求抛物线的解析式;
(2)连接AC,CD,AD,试证明△ACD为直角三角形;
(3)若点E在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F为顶点的四边形为平行四边形?若存在,求出所有满足条件的点F的坐标;若不存在,请说明理由.
在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试验发现,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
某超市销售一种饮料,每瓶进价为4元.经市场调查表明,当售价在5元到8元之间(含5元,8元)浮动时,每瓶售价每增加1元,日均销售量减少40瓶;当售价为每瓶为6元时,日均销售量为120瓶.问:销售价格定为每瓶多少元时,所得日均毛利润(每瓶毛利润=每瓶售价-每瓶进价)最大?最大日均毛利润为多少元?
(1997•西宁)已知二次函数y=ax2+bx+c的图象抛物线G经过(﹣5,0),(0, ),(1,6)三点,直线l的解析式为y=2x﹣3
),(1,6)三点,直线l的解析式为y=2x﹣3
(1)求抛物线G的函数解析式;
(2)求证:抛物线G与直线L无公共点;
(3)若与l平行的直线y=2x+m与抛物线G只有一个公共点P,求P点的坐标.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
某汽车制造厂开发了一款新式电动汽车,计划一年生产安装360辆,由于抽调不出足够的熟练工人来完成新式电动汽车的安装,工厂决定招聘一些新工人,他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:3名熟练工和2名新工人每月可安装24辆电动汽车;2名熟练工和3名新工人每月可安装21辆电动汽车.
(1)每名熟练工和每人新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发3000元的工资,给每名新工人每月发1800元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时支出的工资总额w(元)尽可能少?
为了解甲、乙两种车的刹车距离,经试验发现,甲车的刹车距离s甲是车速v的 ,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
| 车速v(km/h) |
40 |
50 |
| 刹车距离s乙(m) |
12 |
17.5 |
(1)分别求出s甲、s乙与车速v的函数关系式;
(2)若乙车在限速120km/h的高速公路上行驶,乙车的最长刹车距离是多少m?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为80km/g的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过16m,但小于18m,乙车的刹车距离是24m,请你比较两车的速度,并判断哪辆车超速?
如图,已知两条直线a∥b,直线a、b间的距离为h,点M、N在直线a上,MN=x;点P在直线b上,并且x+h=40.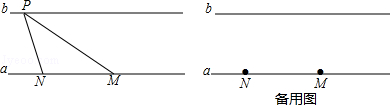
(1)记△PMN的面积为S,
①求S与x的函数关系,并求出MN的长为多少时△PMN的面积最大?最大面积是多少?
②当△PMN的面积最大时,能求出∠PMN的正切值吗?为什么?
(2)请你用尺规作图的方法确定△PMN的周长最小时点P的位置(要求不写作法,但保留作图痕迹);并判断△PMN的形状;
(3)请你在(2)②中得到的△PMN内求一点P,使得AP+AM+AN的和最小,求出AP+AM+AN和的最小值.
某工厂计划为灾区学校生产甲、乙两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套甲型桌椅(一桌两椅)需木料0.5m3,一套乙型桌椅(一桌三椅)需木料0.7m3,工厂现有库存木料302m3.
(1)有多少种生产方案?
(2)现要把生产的全部桌椅运往灾区,已知每套甲型桌椅的生产成本为100元,运费2元;每套乙型桌椅的生产成本为120元,运费4元,求总费用y(元)与生产甲型桌椅x(套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用=生产成本+运费)
某公司对工作五年及以上的员工施行新的绩效考核制度,现拟定工作业绩W=P+1200,其中P的大小与工作数量x(单位)和工作年限n有关(不考虑其他因素).已知P由部分的大小与工作数量x(单位)和工作年限n有关(不考虑其他因素).已知P由两部分的和组成,一部分与x2成正比,另一部分与 nx成正比,在试行过程中得到了如下两组数据:①工作12年的员工,若其工作数量为50单位,则其工作业绩为3700元;②工作16年的员工,若其工作数量为80单位,则其工作业绩为6320元.
nx成正比,在试行过程中得到了如下两组数据:①工作12年的员工,若其工作数量为50单位,则其工作业绩为3700元;②工作16年的员工,若其工作数量为80单位,则其工作业绩为6320元.
(1)试用含x和n的式子表示W;
(2)若某员工的工作业绩为4080元,工作数量为40单位,求该员工的工作年限;
(3)若员工的工作年限为10年,若要使其工作业绩最高,其工作数量应为多少单位?此时他的工作业绩为多少元?
某电器超市销售每台进价分别为200元,170元的A、B联众型号的电风扇,表中是近两周的销售情况:
| 销售时段 |
销售数量 |
销售收入 |
|
| A种型号 |
B种型号 |
||
| 第一周 |
3台 |
5台 |
1800元 |
| 第二周 |
4台 |
10台 |
3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
| x(天) |
1 |
2 |
3 |
… |
50 |
| p(件) |
118 |
116 |
114 |
… |
20 |
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+ .
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M,连接BF与EG交于点P.

(1)当点F与AD的中点重合时(如图1):
①△AEF的边AE= cm,EF= cm,线段EG与BF的大小关系是EG BF;(填“>”、“=”或“<”)
②求△FDM的周长.
(2)当点F在AD边上除点A、D外的任意位置时(如图2):
③试问第(1)题中线段EG与BF的大小关系是否发生变化?请证明你的结论;
④当点F在何位置时,四边形AEGD的面积S最大?最大值是多少?
在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
(1)求点A,B的坐标;
(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;
(3)若该抛物线在-2<x<-1这一段位于直线l的上方,并且在2<x<3这一段位于直线AB的下方,求该抛物线的解析式.