如图,直线l:y=−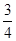 x+6与x轴、y轴分别交于点M,N.点P从点N出发,以每秒1个单位长度的速度沿N→O方向运动,点Q从点O出发,以每秒2个单位长度的速度沿O→M的方向运动.已知点P、Q同时出发,当点Q到达点M时,P、Q两点同时停止运动,设运动时间为t秒.
x+6与x轴、y轴分别交于点M,N.点P从点N出发,以每秒1个单位长度的速度沿N→O方向运动,点Q从点O出发,以每秒2个单位长度的速度沿O→M的方向运动.已知点P、Q同时出发,当点Q到达点M时,P、Q两点同时停止运动,设运动时间为t秒.
(1)直接写出点M,N的坐标;
(2)当t为何值时,PQ与l平行?
(3)设四边形MNPQ的面积为S,求S关于t的函数关系式,并求S的最小值.
(本小题满分9分)某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数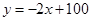 .(利润=售价﹣制造成本)
.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.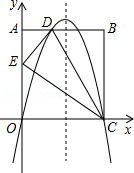
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
在平面直角坐标系xOy中,抛物线 经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
(1)求此抛物线的解析式;
(2)点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
(3)设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM ?若存在,求出点Q的坐标;若不存在,说明理由.
(本小题10分)今年,6月2日为端午节.在端午节前夕,某校的八年级三位同学到超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.
(1)小华的问题解答: ;(2)小明的问题解答: .
(本小题10分)为了落实国务院总理李克强同志的指示精神,市政府出台了一系列“三农”优惠政策,使农民收入大幅增加,某农户生产一种“红颜草莓”,已知这种草莓的成本价为10元/千克.市场调查发现,该产品每天的销售量w(千克)与销售价x(元/千克)有如下关系:w=60-2x,设这种草莓每天的销售利润为y(元).
(1)求y与x之间的函数关系式:
(2)当这种草莓的销售价定为多少时,每天的销售利润最大?最大利润是多少?
(3)若这种草莓从上市开始销售单价x与销售月数m的关系是x=-2m+22(0<m<6,且m为整数),求该农户共获得多少万元利润(每个月按30天计).
(本小题满分12分)清明节期间,两位同学到某超市调查一种进价为2元/只的粽子的情况。请根据对话提供的信息,解答以下问题:
(1)当销售单价是多少元时,每天的销售利润可达到800元?
(2)当销售单价是多少元时,每天的销售利润可达到最大?
注:销售利润=销售量×(销售单价-进价).
用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为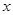 米,面积为
米,面积为 平方米.
平方米.
(1)求 关于
关于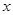 的函数关系式;
的函数关系式;
(2)当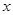 为何值时,围成的养鸡场面积为60平方米?
为何值时,围成的养鸡场面积为60平方米?
(3)能否围成面积为70平方米的养鸡场?如果能,求出其边长;如果不能,说明理由.
已知二次函数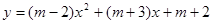 的图像过点(0,5).
的图像过点(0,5).
(1)求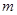 的值,并写出这个二次函数的解析式.
的值,并写出这个二次函数的解析式.
(2)求出该二次函数图像的顶点坐标、对称轴.
在平面直角坐标系xOy中(O为坐标原点),已知抛物线y=x2+bx+c过点A(4,0),B(1,-3).
(1)求出该抛物线的函数解析式;
(2)设该抛物线的对称轴为直线l,点P(m,n)是抛物线上在第一象限的点,点E与点P关于直线l对称,点E与点F关于y轴对称.若四边形OAPF的面积为48,求点P的坐标;
(3)在(2)的条件下,设M是直线l上任意一点,试判断MP+MA是否存在最小值,若存在,求出这个最小值及相应的点M的坐标;若不存在,请说明理由.
已知:函数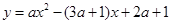 (a为常数).
(a为常数).
(1)若该函数图象与坐标轴只有两个交点,求a的值;
(2)若该函数图象是开口向上的抛物线,与x轴相交于点A(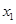 ,0),B(
,0),B(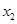 ,0)两点,与y轴相交于点C,且
,0)两点,与y轴相交于点C,且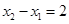 .
.
①求抛物线的解析式;
②作点A关于y轴的对称点D,连结BC,DC,求sin∠DCB的值.
已知抛物线y=ax2+bx+c经过点A(-1,0),且经过直线y=x-3与x轴的交点B及与y轴的交点C.
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标;
(3)若点M在第四象限内的抛物线上,且OM⊥BC,垂足为D,求点M的坐标.
已知二次函数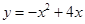 .
.
(1)求函数图象的对称轴和顶点坐标;
(2)求这个函数图象与x轴的交点坐标.
在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量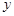 (个)与销售单价
(个)与销售单价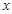 (元/个)之间的对应关系如图所示:
(元/个)之间的对应关系如图所示: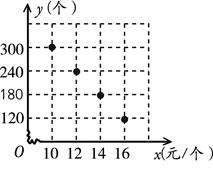
(1)观察图象判断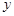 与
与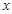 之间的函数关系,并求出函数关系式;
之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润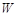 (元)与销售单价
(元)与销售单价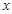 (元/个)之间的函数关系式;
(元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大的利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.