河南省商丘市九年级上学期期末考试数学试卷
下列事件中,是不可能事件的是( )
| A.买一张电影票,座位号是奇数 |
| B.射击运动员射击一次,命中9环 |
| C.明天会下雨 |
| D.度量三角形的内角和,结果是360° |
△ABC与△ 是位似图形,且△ABC与△
是位似图形,且△ABC与△ 的位似比是1︰2,已知△ABC的面积是3,则△
的位似比是1︰2,已知△ABC的面积是3,则△ 的面积是( )
的面积是( )
| A.3 | B.6 | C.9 | D.12 |
如图,点A,B,C在⊙O上,∠A=50°,则∠BOC的度数为( )
| A.40° | B.50° | C.80° | D.100° |
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是()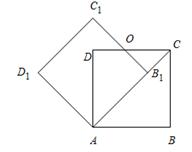
A.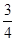 |
B.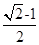 |
C.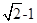 |
D.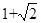 |
一个口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球,然后放回,再随机地摸出一个小球,则两次摸出的小球标号的和等于4的概率是 .
如图,小明用长为3cm的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点O,此时O点与竹竿的距离OD=6m,竹竿与旗杆的距离DB=12m,则旗杆AB的高为 m.
如图,一段抛物线 记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3;…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( )
记为m1,它与x轴交点为O,A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3;…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( )
如图,半径为6cm 的⊙O中,C,D为直径AB 的三等分点,点E,F分别在AB两侧的半圆上,∠BCE =∠BDF = 60°,连结AE,BF.则图中两个阴影部分的面积和为 cm2.
已知二次函数y=x2+2x-1.
(1)写出它的顶点坐标;
(2)当x取何值时,y随x的增大而增大;
(3)求出图象与x轴的交点坐标.
已知:关于x的方程x2﹣(k+2)x+2x=0
(1)求证:无论取任何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长a=1,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.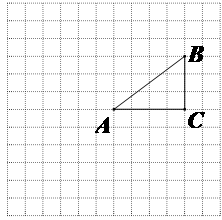
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
如图,有四张背面相同的纸牌A、B、C、D,其正面分别画有四个不同的图形,小明将这四张牌背面朝上洗匀后随机摸出一张,放回后洗匀再随机摸出一张。
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用A、B、C、D表示)
(2)求两次摸牌的牌面图形既是中心对称图形又是轴对称图形的概率。
如图,直线y=mx与双曲线y= 相交于A,B两点,A点坐标为(1,2).
相交于A,B两点,A点坐标为(1,2).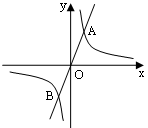
(1)求反比例函数的解析式;
(2)根据函数图像直接写出当mx> 时,x的取值范围;
时,x的取值范围;
(3)计算线段AB的长.
如图,AB是⊙O的直径,点E是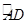 上的一点,∠DBC=∠BED.
上的一点,∠DBC=∠BED.
(1)求证:BC是⊙O的切线;
(2)已知AD=3,CD=2,求BC的长.
已知,如图,A(0.8),B(4,0),D是AB的中点,过D点作直线与△AOB的一边交于点E,直线DE截△ABO得到的小三角形与△ABO相似,求满足题意的所有E点的坐标.
为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
 时,函数
时,函数 的图象在( )
的图象在( ) ,则下列比例式成立的是( )
,则下列比例式成立的是( )



 向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )
向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )



 的常数项为0,则m的值为( )
的常数项为0,则m的值为( ) 的图象如图所示,则二次函数
的图象如图所示,则二次函数 的图象大致为( )
的图象大致为( )

 (k≠0)的图象经过点(2,﹣1),则k的值为 .
(k≠0)的图象经过点(2,﹣1),则k的值为 . 有两个不相等的实数根,则k的取值范围是 .
有两个不相等的实数根,则k的取值范围是 .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号