如图,抛物线y=x2﹣3x﹣18与x轴交于A、B两点,与y轴交于点C,连接BC、AC.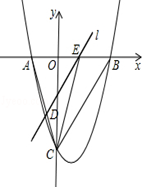
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价1元,其销量就减少20件。
(1)要使每天获得利润700元,请你帮忙确定售价;
(2)问售价定在多少时能使每天获得的利润最多?并求出最大利润。
如图所示,已知平面直角坐标系xOy,抛物线过点A(4,0)、B(1,3)
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.
(本小题满分12分)
如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA="16" cm, OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒2cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用含t的式子表示△OPQ的面积S;
(2)判断四边形OPBQ的面积是否是一个定值,如果是,请求出这个定值;如果不是,请说明理由;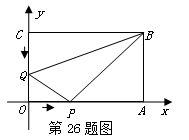 (3)当△OPQ∽△ABP时,抛物线y=
(3)当△OPQ∽△ABP时,抛物线y=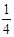 x2+bx+c经过B、P两点,求抛物线的解析式;
x2+bx+c经过B、P两点,求抛物线的解析式;
(4)在(3)的条件下,过线段BP上一动点M作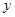 轴的平
轴的平
行线交抛物线于N,求线段MN的最大值.
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图像经过点B、D.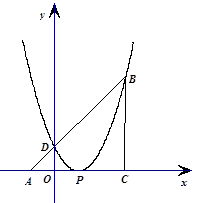
请直接写出用m表示
 点A、D的坐标
点A、D的坐标求这个二次函数的解析式;
点Q为二次函数图像上点P至点B之间的一点,连结PQ、BQ,求四边形ABQP面积的最大值.
如图,已知抛物线 交x轴的正半轴于点A,交y轴于点B.
交x轴的正半轴于点A,交y轴于点B.求A、B两点的坐标,并求直线AB的解析式;
设
 (
( )是直线
)是直线 上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF.若正方形PEQF与直线AB有公共点,求x的取值范围;
上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF.若正方形PEQF与直线AB有公共点,求x的取值范围;在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值.

如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.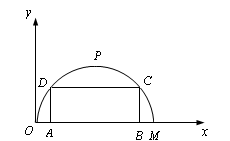
直接写出点M及抛物线顶点P的坐标;
求这条抛物线的解析式;
若要搭建一个矩形“支撑架”AD- DC- CB,
使C、D点在抛物线上,A、B点在地面OM上,
大学生李某投资在沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日采购进一种今年新上市的文具袋.9月份(9月1日至9月30日)进行30天的试销售,购进价格为20
元/个.销售结束后,得知日销售量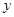 (个)与销售时间
(个)与销售时间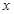 (天)之间有如下关系:
(天)之间有如下关系: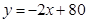 (
(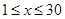 ,且
,且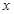 为整数);又知销售价格
为整数);又知销售价格 (元/个)与销售时间
(元/个)与销售时间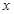 (天)之间的函数关系满足如图所示的函数图像.
(天)之间的函数关系满足如图所示的函数图像.
(1)求 关于
关于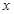 的函数关系式;
的函数关系式;
(2)求出在这30天(9月1日至9月30日)的试销中,日销售利润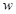 (元)与销售时间
(元)与销售时间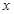 (天)之间的函数关系式;
(天)之间的函数关系式;
(3)“十一”黄金周期间,李某采用降低售价从而提高日销售量的销售策略.10月1日全天,销售价格比9月30日的销售价格降低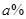 而日销售量就比9月30日提高了
而日销售量就比9月30日提高了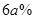 (其中
(其中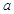 为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求
为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求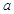 的值.
的值.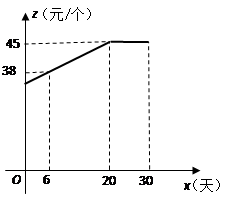 (参考数据:
(参考数据: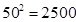 ,
,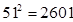 ,
,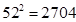 )
)
抛物线 经过A(
经过A(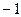 ,0)、C(0,
,0)、C(0,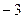 )两点,与
)两点,与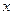 轴交于另一点B。
轴交于另一点B。
(1)求此抛物线的解析式;
(2)已知点D(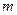 ,
,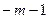 )在第四象限的抛物线上,求点D关于直线BC对称的点
)在第四象限的抛物线上,求点D关于直线BC对称的点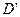 ,的坐标。
,的坐标。
(3)在(2)的条件下,连结BD,问在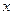 轴上是否存在点P,使
轴上是否存在点P,使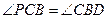 ,若存在,请求出P点的坐标;若不存在,请说明理由
,若存在,请求出P点的坐标;若不存在,请说明理由