初中数学二次函数在给定区间上的最值试题

如图，在平面直角坐标系中，直线与抛物线交于A、B两点，点A在x轴上，点B的横坐标为－8．

（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．
①设△PDE的周长为，点P的横坐标为，求关于的函数关系式，并求出的最大值；
②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在轴上时，求出对应点P的坐标．

如图，在平面直角坐标系xoy中，直线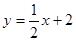与x 轴交于点A，与y轴交于点C．抛物线y=ax²+bx+c的对称轴是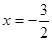且经过A、C两点，与x轴的另一交点为点B．  

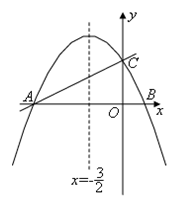
（1）①直接写出点B的坐标；②求抛物线解析式．
（2）若点P为直线AC上方的抛物线上的一点，连接PA，PC．求△PAC的面积的最大值，并求出此时点P的坐标；
（3）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．

如图，直线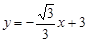与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线与x轴交于另一点A，线段BC与抛物线的对称轴l相交于点D，设抛物线的顶点为P，连接AD，线段AD与y轴相交于点E．

（1）求该抛物线的解析式及对称轴；
（2）连结AP，请在y轴正半轴上找一点Q，使Q、C、D为顶点的三角形与△ADP全等，并求出点Q的坐标．将∠CED绕点E顺时针旋转，边EC旋转后与线段BC相交于点M，边ED旋转后与对称轴l相交于点N，若2DM=DN，求点M的坐标．

如图，直线y=kx+c与抛物线y=ax²+bx+c的图象都经过y轴上的D点，抛物线与x轴交于A、B两点，其对称轴为直线x=1，且OA=OD．直线y=kx+c与x轴交于点C（点C在点B的右侧）．则下列命题中正确命题的个数是（ ）
①abc＞0；②3a+b＞0；③﹣1＜k＜0；④k＞a+b；⑤ac+k＞0．

A．1    B．2    C．3    D．4

已知抛物线与轴交于点，且．

（1）求抛物线的解析式．
（2）抛物线的对称轴为，与y轴的交点为C，顶点为D，点C关于的对称点为E．是否存在x轴上的点M、y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．
（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形
时，求点P的坐标。

如图，在相距2米的两棵树间拴一根绳子做一个简易的秋千．拴绳子的地方距地面高都是2．5米，绳子自然下垂呈抛物线状，身高1米的小芳距较近的那棵树0．5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为       米．

如图，已知二次函数L₁:y=ax²-2ax+a+3（a＞0）和二次函数L₂:y=-a（x+1）²+1（a＞0）图象的顶点分别为M，N ， 与轴分别交于点E， F．

（1） 函数的最小值为             ；
当二次函数L₁ ，L₂的值同时随着的增大而减小时，的取值范围是                ；
（2）当时，求的值，并判断四边形的形状（直接写出，不必证明）；
（3）若二次函数L₂的图象与轴的右交点为，当△为等腰三角形时，求方程的解．

如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y₁和过P、A两点的二次函数y₂的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=3时，这两个二次函数的最大值之和等于（   ）

A．      B．      C．3      D．4

如图，抛物线y=ax²+bx+3经过A（﹣1，0），B（3，0）两点，且交y轴于点C，对称轴与抛物线相交于点P、与直线BC相交于点M．

（1）求该抛物线的解析式．
（2）在抛物线上是否存在一点N，使得|MN﹣ON|的值最大？若存在，请求出点N的坐标；若不存在，请说明理由．
（3）连接PB，请探究：在抛物线上是否存在一点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．

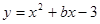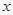如图1：矩形OABC的顶点A、B在抛物线上，OC在轴上，且．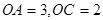
（1）求抛物线的解析式及抛物线的对称轴．
（2）如图2，边长为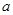的正方形ABCD的边CD在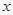轴上，A、B两点在抛物线上，请用含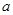的代数式表示点B的坐标,并求出正方形边长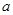的值．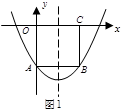

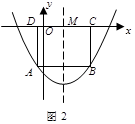
定义一种变换：平移抛物线F₁得到抛物线F₂，使F₂经过F₁的顶点A．设F₂的对称轴分别交F₁，F₂于点D，B，点C是点A关于直线BD的对称点．

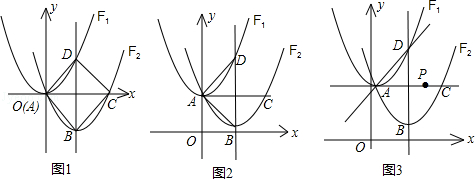
（1）如图1，若F₁：y=x²，经过变换后，得到F₂：y=x²+bx，点C的坐标为（2，0），则：
①b的值等于      ；
②四边形ABCD为（ ）
A、平行四边形；B、矩形；C、菱形；D、正方形．
（2）如图2，若F₁：y=ax²+c，经过变换后，点B的坐标为（2，c﹣1），求△ABD的面积；
（3）如图3，若F₁：y=x²﹣x+，经过变换后，AC=2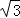，点P是直线AC上的动点，求点P到点D的距离和到直线AD的距离之和的最小值．

已知抛物线y=ax²+2x+c与x轴交于A（1，0）和点B，与y轴交于点C（0，﹣3）．
（1）求抛物线的解析式．
（2）如图1，已知点H的坐标为（0，1），设点M为y轴左侧抛物线上的一个动点，试猜想：是否存在这样的点M，使|MA﹣MH|的值最大，如果存在，请求出点M的坐标；如果不存在，请说明理由．
（3）如图2，过x轴上点E（﹣2，0）作ED⊥AB交抛物线于点D，在y轴上找一点F，使△EDF的周长最小，求出此时点F的坐标；
（4）如图3，已知点N（0，﹣1）．问在抛物线上是否存在点Q（点Q在y轴的左侧），使得△QNC的面积与△QNA的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，抛物线与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

（1）求该抛物线的解析式；
（2）当点P在直线BC上方时，请用含m的代数式表示PG的长度；
（3）在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．

“双十一”淘宝网销售一款工艺品，每件的成本是50元．销售期间发现：销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件．但要求销售单价不得低于成本．设当销售单价为x元时，每天的销售利润为y元．
（1）求出y与x之间的函数表达式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果每天的销售利润不低于4000元，那么每天的总成本至少需要             元．
（每天的总成本=每件的成本×每天的销售量）

若一个三角形的三个顶点均在一个图形的不同的边上，则称此三角形为该图形的内接三角形．

（1）在图①中画出△ABC的一个内接直角三角形；
（2）如图②，已知△ABC中，∠BAC＝60°，∠B＝45°，AB＝8，AD为BC边上的高，探究以D为一个顶点作△ABC的内接三角形，其周长是否存在最小值？若存在，请求出最小值；若不存在，请说明理由；
（3）如图③，△ABC为等腰直角三角形，∠C＝90°，AC＝６，试探究：△ABC的内接等腰直角三角形的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．