如图为二次函数
的图象，此图象与
轴的交点坐标分别为（
）、（3，0）.下列说法正确的个数是 （ ）
①
②
③方程
的根为
，
④当
时，
随着的增大而增大
| A．1 | B．2 | C．3 | D．4 |
小明从二次函数y=ax2+bx+c的图象（如图）中观察得出了下面五条信息：①c＜0；
②abc＞0；③a-b+c＞0；④2a-3b=0；⑤c-4b＞0.你认为其中正确的信息是（ ）
| A．①②③⑤ | B．①②③④ |
| C．①③④⑤ | D．②③④⑤ |
已知抛物线m：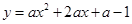
，顶点为A，若将抛物线m绕着点（1，0）旋转180°后得到抛物线n，顶点为C.当a=1时.试求抛物线n的顶点C的坐标，再求它的解析式；
在（1）中，请你分别在抛物线m、n上各取一点D、B（除点A、C外），
使得四边形ABCD为平行四边形（直接写出所取点的坐标，并至少写出二种情况）；设抛物线m的对称轴与抛物线n的交点为P，且
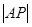=6，试求a的值.
矩形OABC的顶点A(-8，0)、C(0，6) ，点D是BC边上的中点，抛物线
经过A、D两点，如图所示．求点D关于y轴的对称点
的坐标及a、b的值；在y轴上取一点P, 使PA+PD长度最短, 求点P的坐标；
将抛物线
向下平移,记平移后点A的对应点为
，点D的对应点为
，当抛物线平移到某个位置时，恰好使得点O是y轴上到
两点距离之和
最短的一点，求此抛物线的解析式．
对于抛物线
，下列说法错误的是（ ）
A．若顶点在x轴下方，则一元二次方程 有两个不相等的实数根 |
| B．若抛物线经过原点，则一元二次方程必有一根为0 |
C．若 ，则抛物线的对称轴必在y轴的左侧 |
D．若 ，则一元二次方程，必有一根为-2 |
如图①，在平面直角坐标系中，已知△ABC是等边三角形，点B的坐标为（12，0），动点P在线段AB上从点A向点B以每秒
个单位的速度运动，设运动时间为t秒．以点P为顶点，作等边△PMN，点M，N在x轴上．
当t为何值时，点M与点O重合．
求点P坐标和等边△PMN的边长（用t的代数式表示）．
如果取OB的中点D，以OD为边在△AOB内部作如图②所示的矩形ODEF，点E在线段AB上．设等边△PMN和矩形ODEF重叠部分的面积为S，请求出当
秒时S与
的函数关系式，并求出S的最大值．
某市种植某种绿色蔬菜，全部用来出口．为了扩大出口规模，该市决定对这种蔬菜的种植实行政府补贴，规定每种植一亩这种蔬菜一次性补贴菜农若干元．经调查，种植亩数
（亩）与补贴数额
（元）之间大致满足如图1所示的一次函数关系．随着补贴数额的不断增大，出口量也不断增加，但每亩蔬菜的收益
（元）会相应降低，且与之间也大致满足如图2所示的一次函数关系．在政府未出台补贴措施前，该市种植这种蔬菜的总收益额为多少？
求政府补贴政策实施后，种植亩数
、每亩蔬菜的收益分别与政府补贴数额之间的函数关系式；要使全市种植这种蔬菜的总收益
（元）最大，政府应将每亩补贴数额定为多少？并求出总收益的最大值．
把抛物线
的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式为
，则
的值为（ ）
| A．9 | B．12 | C． |
D．10 |
抛物线y＝x2－4x－5的顶点在第_____象限．（ ）
| A．一 | B．二 | C．三 | D．四 |
如图，已知
的顶点
，
，
是坐标原点．将绕点按逆时针旋转90°得到
．写出
两点的坐标；求过
三点的抛物线的解析式，并求此抛物线的顶点
的坐标；在线段
上是否存在点
使得
？若存在，请求出点的坐标；
若不存在，请说明理由．
已知二次函数
． (1)用配方法将函数解析式化为y=a(x-h)2+k的形式；
(2)当x为何值时，函数值y=0；
(3)列表描点，在所给坐标系中画出该函数的图象；
(4)观察图象，指出使函数值
y＞
时自变量x的取值范围．
粤公网安备 44130202000953号
的图像与
轴有两个交点，则
的取值范围是 （ ）
：
与抛物线
关于
轴对称，则抛物线
与x轴交于不同的两点，则
的取值范围是 ____．
向上平移2个单位后，所得抛物线的解析式是（ ）
