初中数学二次函数在给定区间上的最值试题

．抛物线如图所示，则它关于轴对称的抛物线的解析式是           ．

已知抛物线y=ax²+bx+c（a0）与x轴的两交点的横坐标分别是-1和3，与y轴交点的纵坐标是－；
（1）确定抛物线的解析式；
（2）说出抛物线的开口方向，对称轴和顶点坐标。

已知抛物线y=x²+bx+c的部分图象如图所示，若y<0,则x的取值范围是         。
第14题

已知函数y=(m+2)x^m(m+1)是二次函数,则m=______________。

若点(2，5)，(4，5)在抛物线y＝ax²＋bx＋c上，则它的对称轴是(    )

A．

B．x＝1

C．x＝2

D．x＝3

把二次函数y=用配方法化成y=a(x-h)²+k的形式（   ）

A．	B．
C．	D．

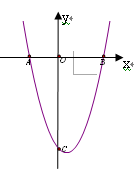
如图，抛物线y＝x²－x＋a与x轴交于点A，B，与y轴交于点C，其顶点在直线y＝－2x上．
求a的值；
求A，B的坐标；
以AC，CB为一组邻边作□ACBD，则点D关于x轴的对称点D′ 是否在该抛物线上？请说明理由．

抛物线的顶点坐标是（ ▲ ）

A．（2，3）

B．（–2，3）

C．（2，–3）

D．（–2，–3）

二次函数y＝( x－1)²+1的图象的顶点坐标是　　　　　.

已知：二次函数的图象经过原点，对称轴是直线＝－2，最高点的纵坐标为4，求：该二次函数解析式。

如图，在中，∠C=90°，AB=5cm，BC=3cm，动点P从点A出发，以每秒1cm的速度，沿ABC的方向运动，到达点C时停止.设,运动时间为t秒，则能反映y与t之间函数关系的大致图象是（   ）

将抛物线向上平移2个单位, 再向右平移3个单位，所得抛物线的解析式为（   ）．

A．	B．
C．	D．

已知抛物线在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（　　）

A．	B．
C．	D．

抛物线y＝2x²－bx＋3的对称轴是直线x＝l，则b的值为  _______

在直角坐标系中，抛物线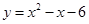与x轴交于点A，B（点A在点B的左侧），与y轴交于点C。如果点M在y轴的右侧的抛物线上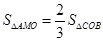，，那么点M的坐标为