二次函数y=ax2+bx+c与一次函数y=ax+c,它们在同一直角坐标系中的图像是( )
抛物线 上部分点的横坐标x,纵坐标y的对应值如表所示,给出下列说法:
上部分点的横坐标x,纵坐标y的对应值如表所示,给出下列说法:
抛物线与y轴的交点为(0,6); ②抛物线的对称轴是在y轴右侧;
③在对称轴左侧,y随x增大而减小;④抛物线一定过点(3, 0).
上述说法正确的是 (填序号).
如图,关于抛物线 ,下列说法错误的是 ( )
,下列说法错误的是 ( )
A.顶点坐标为(1, ) ) |
| B.对称轴是直线x=l |
| C.开口方向向上 |
| D.当x>1时,Y随X的增大而减小 |
已知二次函数 的顶点为A,与y轴交于点B,作以P(1,0)为中心的中心对称的图像顶点为C,交y轴于点D,则四边形ABCD面积为________.
的顶点为A,与y轴交于点B,作以P(1,0)为中心的中心对称的图像顶点为C,交y轴于点D,则四边形ABCD面积为________.
已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)
(1)求该函数的关系式;
(2)求该函数图象与坐标轴的交点坐标;
(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A1、B2,求△OA1B2的面积。
如图,在平面直角坐标系中,抛物线 与x轴交于A、B两点,点A在x轴负半轴,点B在x轴正半轴,与y轴交于点C,且tan∠ACO=
与x轴交于A、B两点,点A在x轴负半轴,点B在x轴正半轴,与y轴交于点C,且tan∠ACO= ,CO=BO,AB=3,则抛物线解析式为 。
,CO=BO,AB=3,则抛物线解析式为 。
抛物线的顶点是C(2, ),它与x轴交于A、B两点,它们的横坐标是方程x2-4x+3=0的两个根,则AB= ,S△ABC= 。
),它与x轴交于A、B两点,它们的横坐标是方程x2-4x+3=0的两个根,则AB= ,S△ABC= 。
生产季节性产品的企业,当它的产品无利润时就会及时停产,现有一生产季节性产品的企业,其一年中获得的利润y和月份n之间的关系式为 ,则该企业一年中应停产的月份时(▲)
,则该企业一年中应停产的月份时(▲)
| A.1月、2月、3月 | B.2月、3月、4月 |
| C.1月、2月、12月 | D.1月、11月、12月 |
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+b+c<0 ②a-b+c>0 ③abc>0④b=2a其中正确的结论有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,抛物线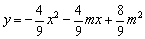 (
(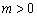 )与
)与 轴相交于
轴相交于 两点,点
两点,点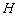 是抛物线的顶点,以
是抛物线的顶点,以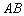 为直径作圆
为直径作圆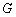 交
交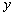 轴于
轴于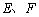 两点,
两点,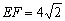 .
.用含
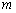 的代数式表示圆
的代数式表示圆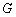 的半径
的半径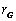 的长;
的长;