2011-2012学年九年级上学期期中考试数学卷
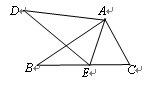
如图,已知D、E分别是 的AB、 AC边上的点,
的AB、 AC边上的点, 且
且 那么
那么 等于( )
等于( )
| A.1 :9 | B.1 :3 | C.1 :8 | D.1 :2 |
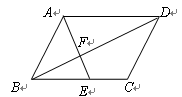
如图,在□ABCD中,E是BC的中点,且∠AEC=∠DCE,下列结论不正确的是( )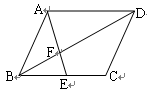
A.BF=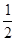 DF DF |
B.S△FAD=2S△FBE | C.四边形AECD是等腰梯形 | D.∠AEB=∠ADC |
△ABC中,BC=54cm,CA=45cm,AB=63cm;另一个和它相似的三角形最短边长为15cm,则最长边一定是( )
A. 18cm B.21cm C 24cm D. 19.5cm
抛物线 与x轴相交,其中一个交点的横坐标是p.那么该抛物线的顶点的坐标是( ).
与x轴相交,其中一个交点的横坐标是p.那么该抛物线的顶点的坐标是( ).
| A. (0,-2) | B. |
C. |
D. |
如图,在平面直角坐标系中,以P (4,6)为位似中心,把△ABC缩小得到△DEF,若变换后,点A、B的对应点分别为点D、E,则点C的对应点F的坐标应为( ).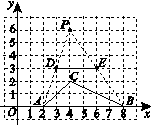
| A.(4,2) | B.(4,4) | C.(4,5) | D.(5,4) |
利用相似三角形可以计算不能直接测量的物体的高度,阳阳的身高是1.6m,他在阳光下的影长是1.2m,在同一时刻测得某棵树的影长为3.6m,则这棵树的高度约为 m.
如图,在△ABC中,M、N是AB、BC的中点,AN、CM交于点O,那么△MON∽△AOC面积的比是____________.
为确保信息安全,信息需要加密传输,发送方由 , 接收方由
, 接收方由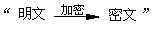 .已知加密规则为:当明文a³1时,a对应的密文为a2-2a+1;当明文a<1时,a对应的密文为-a2+2a-1. 例如:明文2对应的密文是 22-2×2+1=1;明文-1对应的密文是-(-1)2+2×(-1)-1=-4. 如果接收方收到的密文为4和-16,则对应的明文分别是 和 .
.已知加密规则为:当明文a³1时,a对应的密文为a2-2a+1;当明文a<1时,a对应的密文为-a2+2a-1. 例如:明文2对应的密文是 22-2×2+1=1;明文-1对应的密文是-(-1)2+2×(-1)-1=-4. 如果接收方收到的密文为4和-16,则对应的明文分别是 和 .
如图,在平面直角坐标系中有两点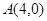 、
、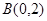 ,如果点
,如果点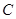 在
在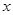 轴上(
轴上(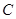 与
与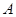 不重合),当点
不重合),当点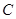 的坐标为
的坐标为
或 时,使得由点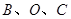 组成的三角形与
组成的三角形与 相似(至少找出两个满足条件的点的坐标).
相似(至少找出两个满足条件的点的坐标).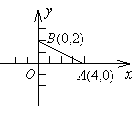
在直角坐标系中,抛物线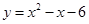 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C。如果点M在y轴的右侧的抛物线上,
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C。如果点M在y轴的右侧的抛物线上,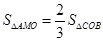 ,那么点M的坐标为
,那么点M的坐标为 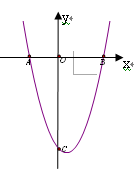
(1)在方格纸中,画出将三角形绕原点O逆时针旋转90°后得到的图形;
(2)在方格纸中,将原三角形以点O为位似中心放大,使它们的位似比为1:2,画出放大后三角形.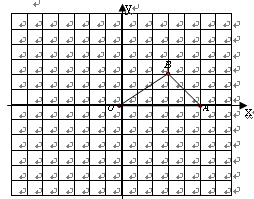
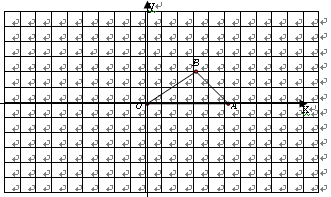
已知:如图,在Rt△ABC中,∠C=90°, D、E分别为AB、 AC边上的点,且 ,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.
,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.
已知:抛物线 (
( 为常数,且
为常数,且 ).
).
(1)求证:抛物线与 轴有两个交点;
轴有两个交点;
(2)设抛物线与 轴的两个交点分别为
轴的两个交点分别为 、
、 (
( 在
在 左侧),与
左侧),与 轴的交点为
轴的交点为 .
.
当 时,求抛物线的解析式;
时,求抛物线的解析式;
如图,抛物线y=-x2+bx+c与x轴、y轴分别交于A(-1,0)、B(0,3)两点,顶点为D.
(1)求该抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积(3分)
(3)AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
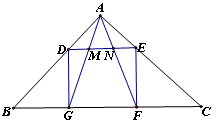
已知:正方形 中,
中, ,
, 绕点
绕点 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交 (或它们的延长线)于点
(或它们的延长线)于点 .当
.当 绕点
绕点 旋转到
旋转到 时(如图1),易证
时(如图1),易证 .
.
(1)当 绕点
绕点 旋转到
旋转到 时(如图2),线段
时(如图2),线段 和
和 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当 绕点
绕点 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段 和
和 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
 的值是( )
的值是( )






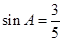 ,那么
,那么 的值等于( )
的值等于( ) B.
B. 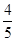 C.
C. 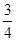 D.
D. 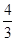
 中,
中, ,
, ,
, ,则
,则 ______
______
 中,
中,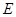 是边
是边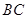 上的点,
上的点,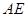 交
交 于点
于点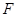 ,如果
,如果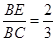 ,那么
,那么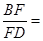 .
.
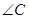 为直角,
为直角,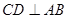 于
于 ,
,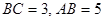 , DB = , CD =
, DB = , CD = 
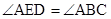 ,若DE=3,BC=6,AB=8,则AE的长
,若DE=3,BC=6,AB=8,则AE的长 为
为 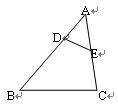
 (2)
(2) 
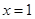 为对称轴的抛物线过点(3,0),(0,3),求此抛物线的解析式.(3分)
为对称轴的抛物线过点(3,0),(0,3),求此抛物线的解析式.(3分)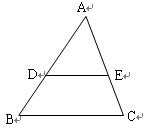
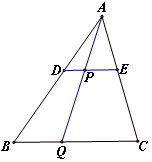
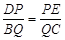 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号