[江苏]2011-2012学年苏州工业园区九年级下学期学科调研数学卷
为了响应中央号召,2011年某市加大财政支农力度,全市农业支出累计将达到530 000 000元,其中530 000 000元用科学记数法可表示为
| A.53×107元 | B.53×108元 | C.5.3×107元 | D.5.3×108元 |
估计58的立方根的大小在( )
| A.2与3之间 | B.3与4之间 | C.4与5之间 | D.5与6之间 |
如图,点A的坐标为(1,0),点B在直线上运动,当线段AB最短时,点B的坐标为 ( )
| A.(0,0) | B.(- , , ) ) |
C.( ,- ,- ) ) |
D.( ,- ,- ) ) |
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.给出下列说法:
| x |
… |
-3 |
-2 |
-1 |
0 |
1 |
2 |
… |
| y |
… |
-6 |
0 |
4 |
6 |
6 |
4 |
… |
①抛物线与y轴的交点为(0,6);②抛物线的对称轴是在y轴的右侧;③抛物线一定经过点(3,0);④在对称轴左侧,y随x增大而减小.从表可知,下列说法正确的个数有( )
A.1个 B.2个 C.3个 D.4个
如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.
求证:(1)△ABC≌△DEF; (2)GF=GC.
.已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
某花农培育甲种花木2株,乙种花木3株,共需成本1700元;培育甲种花木3株,乙种花木1株,共需成本1500元.
(1)求甲、乙两种花木每株成本分别为多少元;
(2)据市场调研,1株甲种花木的售价为760元,1株乙种花木的售价为540元,该花农决定在成本不超过30000元的前提下培育甲乙两种花木,若培育乙种花木的株数是甲种花木的3倍还多10株,那么要使总利润不少于21600元,花农有哪几种具体的培育方案?
已如图,反比例函数y=的图象与一次函数y=mx+b的图象交于两点A(1,3) ,B(n,-1).
(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,直接回答:当x取何值时,一次函数的值大于反比例函数的值;答:
(3) 连接AO、BO,求△ABO的面积;
如图,矩形ABCD,AB=6cm,AD=2cm,点P以2cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以lcm/s的速度从顶点C出发向点D运动,当其中一个动点到达末端停止运动时,另一点也停止运动.
(1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的 ;
;
(2)问两动点经过多长时间使得点P与点Q之间的距离为 ?若存在,求出运动所需的时间;若不存在,请说明理由.
?若存在,求出运动所需的时间;若不存在,请说明理由.
如图,直线y=x-1和抛物线y=x 2+bx+c都经过点A(1,0),B(3,2).
(1)求抛物线的解析式;
(2)求不等式x2+bx+c<x-1的解集(直接写出答案).
(3)设直线AB交抛物线对称轴与点D,请在对称轴上求一点P(D点除外),使△PBD为
等腰三角形.(直接写出点P的坐标,不写过程)







 ,则
,则 的值为 ____
的值为 ____ 
 的值等于______
的值等于______ 的解是正数,则a的取值范围是 ____
的解是正数,则a的取值范围是 ____  的部分图象如图所示,则一元二次方程
的部分图象如图所示,则一元二次方程 的根为 .
的根为 .


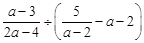 ,其中a=
,其中a=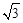 -3.
-3.
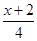 ≤
≤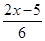 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来
 粤公网安备 44130202000953号
粤公网安备 44130202000953号