初中数学二次函数在给定区间上的最值试题

如图4，一次函数y₁=mx＋n（m≠0）与二次函数y₂=ax²＋bx＋c（a≠0）的图象相交于两点A（－1，5）、B（9，3），请你根据图象写出使y₁≥y₂成立的x的取值范围

A．－1≤x≤9	B．－1≤x＜9
C．－1＜x≤9	D．x≤－1或x≥9

已知二次函数y =" -" x² - x +
在给定的直角坐标系中，画出这个函数的图象；

根据图象，写出当y ＜ 0时，x的取值范围
若将此图象沿x轴向右平移3个单位，请写出平移后图象所对应的函数关系式

若二次函数的对称轴是过（1，0）且与x轴垂直的直线，且部分图象如图16所示，则关于x的一元二次方程的一个解，另一个解  ▲   ；

已知二次函数（k为常数）的图象与x轴的一个交点坐标为（1,0），则与x轴的另一个交点坐标为         ．

若二次函数．当≤l时，随的增大而减小，则的取值范围是(    )

A．=l

B．>l

C．≥l

D．≤l

已知二次函数y=ax2+bx+c，当x=-1时有最小值-4，且图象在x轴上截得线段长为4，求函数解析式．

已知二次函数，若－1≤x≤6， 则y的取值范围为__ ▲ __．

如图，直线y=3x+3与 x轴、y轴分别交于点B、A，O为原点，ΔAOB绕点O顺时针方向旋转90^o后得到ΔCOD。
求A、B、C、D四点的坐标
求经过A、B、C、三点的抛物线的解析式
设E为抛物线的顶点，连接DE，在线段DE上是否存在点P，使得以C、D、P为顶点的三角形与ΔDOC相似？若存在，求出点P的坐标，若不存在，请说明理由。

已知二次函数y=x²+bx-2的图象与x轴的一个交点为（1，0），则抛物线与x轴的另一个交点的坐标是      。

四边形ABCD是平行四边形，AB=3，AD= 5，高DE=2．建立如图所示的平面直角坐标系，其中点A与坐标原点O重合．
求BC边所在直线的解析式；
设点F为直线BC与y轴的交点，求经过点B，D，F的抛物线解析式；
判断▱ABCD的对角线的交点G是否在（2）中的抛物线上，并说明理由．

反比例函数的图象如左图所示，那么二次函数y = kx²－k²x —1图象大致为

函数在同一直角坐标系内的图象大致是(   )

二次函数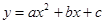的图象如图所示，则一次函数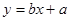的图象不经过（         ）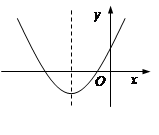

A．第一象限

B．第二象限

C．第三象限

D．第四象限

若A（-5，），B（-3，），C（0，）为二次函数的图象上的三点，则、、的大小关系是（★）   

A．＜＜

B．

C．

D．

在平面直角坐标系xOy中，抛物线经过点N（2,－5），过点N作x轴的平行线交此抛物线左侧于点M，MN=6.
求此抛物线的解析式
点P（x,y）为此抛物线上一动点，连接MP交此抛物线的对称轴于点D，当△DMN为直角三角形时，求点P的坐标；
设此抛物线与y轴交于点C，在此抛物线上是否存在点Q，使∠QMN=∠CNM ？若存在，求出点Q的坐标；若不存在，说明理由.