[江苏]2012年江苏省太仓市初中毕业暨升学考试模拟数学试卷
下面四个由−2和3组成的算式中,运算值最小的是( ▲ )
| A.−2− 3 | B.−2 ´ 3 | C.3−2 | D.(−3)2 |
一个正方形的面积为28,则它的边长应在( ▲ )
| A.3到4之间 | B.4到5之间 | C.5到6之间 | D.6到7之间 |
一组数据4,5,6,7,7,8的中位数和众数分别是( ▲ )
| A.7,7 | B.7,6.5 | C.5.5,7 | D.6.5,7 |
如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是−1,则顶点A坐标是( ▲ )
| A.(2,−1) | B.(1,−2) | C.(1,2) | D.(2,1) |

如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( ▲ )
A.AD∥BC B.AC⊥BD
C.四边形ABCD面积为 D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形
如图,等边三角形ABC中,D为BC的中点,BE平分∠ABC交AD于E,若△CDE的面积等于1,则△ABC的面积等于( )
A 2 B.4 C.6 D.12 
已知P是⊙O内一点,⊙O的半径为15,P点到圆心O的距离为9,则通过P点且长度是整数的弦的条数是( ▲ )
| A.5 | B.7 | C.10 | D.12 |
△ABC中,∠ABC=30°,边AB=10,边AC可以从4,5,7,9,11取一值.满足这些条件的互不全等三角形的个数是( )
| A.6 | B.7 | C.5 | D.4 |
去年,太仓全市实现全口径财政收入226.5亿元,同比增长25.8%.则226.5亿元用科学记数法可表示为 ▲ 元.
已知二次函数y=ax2+bx+c,当x=-1时有最小值-4,且图象在x轴上截得线段长为4,求函数解析式.
如图,直线y=  与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O,若将⊙P沿x轴向左平平移,当⊙P向左平移 个单位长度时,⊙P与该直线相切.
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O,若将⊙P沿x轴向左平平移,当⊙P向左平移 个单位长度时,⊙P与该直线相切. 
如图,已知四边形ABCD的对角线AC、BD相交于点O,△ABC≌△BAD.
求证:OA=OB;
若∠CAB=35°,求∠CDB的度数.
太仓人杰地灵,为了了解学生对家乡历史文化名人的知晓情况,某校对部分学生进行了随机抽样调查,并将调查结果绘制成如图所示统计图的一部分.
根据统计图中的信息,回答下列问题:
本次抽样调查的样本容量是 ▲ _;
在扇形统计图中,“了解很少”所在扇形的圆心角是 ▲ 度;
若全校共有学生1300人,那么该校约有多少名学生“基本了解”太仓的历史文化名人?

我们在配平化学方程式时,对于某些简单的方程式可以用观察法配平,对于某些复杂的方程式,还可以尝试运用方程的思想和比例的方法.例如方程式: ,可以设NH3的系数为1,其余三项系数分别为x、y、z,即:
,可以设NH3的系数为1,其余三项系数分别为x、y、z,即: ,依据反应前后各元素守恒,得:
,依据反应前后各元素守恒,得: ,解之得四项系数之比为1:
,解之得四项系数之比为1: :1:
:1: ,扩大4倍得整数比为4:5:4:6,即配平结果为:
,扩大4倍得整数比为4:5:4:6,即配平结果为: .请运用上述方法,配平化学方程式:
.请运用上述方法,配平化学方程式: .
.
智能手机如果安装了一款测量软件“Smart Measure”后,就可以测量物高、宽度和面积等.如图,打开软件后将手机摄像头的屏幕准星对准脚部按键,再对准头部按键,即可测量出人体的高度.其数学原理如图②所示,测量者AB与被测量者CD都垂直于地面BC.若手机显示AC = 1m,AD = 1.8m,∠CAD = 60°,求此时CD的高.(结果保留根号)
对于一般情况,试探索手机设定的测量高度的公式:设AC= a,AD= b,∠CAD= α,即用a、b、α来表示CD.(提示:sin2α+ cos2α= 1)

如图,已知一次函数y1 = k1x + 6与反比例函数 (x>0)的图象交于点A、B,且A、B两点的横坐标分别为2和4.
(x>0)的图象交于点A、B,且A、B两点的横坐标分别为2和4.k1= ▲ ,k2= ▲ ;
求点A、B、O所构成的三角形的面积;
对于x>0,试探索y1与y2的大小关系(直接写出结果).

如图,已知矩形ABCD中,AB=10,AD=4,点E为CD边上的一个动点,连结AE、BE,以AE为直径作圆,交AB于点F,过点F作FH⊥BE于H,直线FH交⊙O于点G.求证:⊙O必经过点D;
若点E运动到CD的中点,试证明:此时FH为⊙O的切线;
当点E运动到某处时,AE∥FH,求此时GF的长.

如图,将□OABC放置在平面直角坐标系xOy内,已知AB边所在直线的解析为:y = − x + 4.点C的坐标是( ▲ , ▲ )
若将□OABC绕点O逆时针旋转90°得OBDE,BD交OC于点P,求△OBP的面积;
在(2)的情形下,若再将四边形OBDE沿y轴正方向平移,设平移的距离为x(0≤x≤8),与□OABC重叠部分面积为S,试写出S关于x的函数关系式,并求出S的最大值.

 的解集是( ▲ )
的解集是( ▲ ) 与
与 有一个解相同,则a的值为( ▲ )
有一个解相同,则a的值为( ▲ )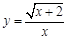 中,自变量x的取值范围是 ▲ .
中,自变量x的取值范围是 ▲ .
 .
.
 ,再从−2,0,1,2中选择一个合适的数代入,求出这个代数式的值.
,再从−2,0,1,2中选择一个合适的数代入,求出这个代数式的值. x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号