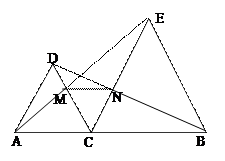
如图,已知点A(−3,5)在抛物线y= x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
求抛物线的解析式;
当A、Q、B三点构成以AQ为直角边的直角三角形时,求点P离开点Q多少时间?
试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)时,点P离开点Q的时刻.

相关知识点
推荐套卷


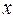 辆,租车总费用
辆,租车总费用 元.
元.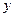 (L)随行驶里程
(L)随行驶里程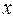 (km)的增加而减少,平均耗油量为0.11L/km.
(km)的增加而减少,平均耗油量为0.11L/km.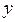 与
与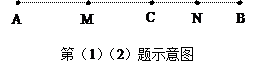
 粤公网安备 44130202000953号
粤公网安备 44130202000953号