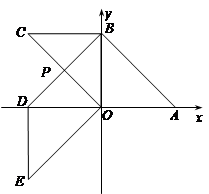如图，将□OABC放置在平面直角坐标系xOy内，已知AB边所在直线的解析为：y = − x + 4．点C的坐标是（ ▲ ， ▲ ）
若将□OABC绕点O逆时针旋转90°得OBDE，BD交OC于点P，求△OBP的面积；
在(2)的情形下，若再将四边形OBDE沿y轴正方向平移，设平移的距离为x（0≤x≤8），与□OABC重叠部分面积为S，试写出S关于x的函数关系式，并求出S的最大值．
轮（即每个队均需要赛
分，平一场得
分，负一场得
分．在这次足球联赛中，雄师队踢平的场数是所负场所的
倍，共得
分．你知道雄师队胜了几场球吗？
（用加减法）
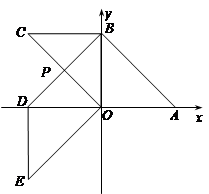
（用代入法）相关知识点
推荐套卷
如图，将□OABC放置在平面直角坐标系xOy内，已知AB边所在直线的解析为：y = − x + 4．点C的坐标是（ ▲ ， ▲ ）
若将□OABC绕点O逆时针旋转90°得OBDE，BD交OC于点P，求△OBP的面积；
在(2)的情形下，若再将四边形OBDE沿y轴正方向平移，设平移的距离为x（0≤x≤8），与□OABC重叠部分面积为S，试写出S关于x的函数关系式，并求出S的最大值．
粤公网安备 44130202000953号