初中数学二次函数在给定区间上的最值试题

在平面直角坐标系中，形如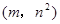的点涂上红色（其中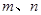为整数），称为红点，其余不涂色，那么抛物线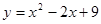上一共有红点

A．2个

B．4个

C．6个

D．无数个

如图，A₁、A₂、A₃是抛物线（ a>0）上的三点，A₁B₁、A₂B₂、A₃B₃分别垂直于轴，垂足为B₁、B₂、B₃，直线A₂B₂交线段A₁A₃于点C，A₁、A₂、A₃三点的横坐标为连续整数n-1、n、n+1,则线段CA₂的长为  ★   ．

二次函数的图像如图所示，反比列函数与正比列函数在同一坐标系内的大致图像是（   ）

若二次函数y=x²﹣6x+c的图象过A（﹣1，y₁），B（2，y₂），C（，y₃），则y₁，y₂，y₃的大小关系是（　▲　）

A．y1＞y2＞y3

B．y1＞y3＞y2

C．y2＞y1＞y3

D．y3＞y1＞y2

如图，抛物线，OA=OC，下列关系中正确的是

A．ac+1=b

B．ab+1=c

C．bc+1="a"

D．

将二次函数配方成的形式为           。

已知抛物线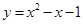与x轴的一个交点为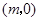，则代数式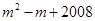的值为（   ）

A．2008

B．2009

C．2011

D．2012

已知二次函数．

当时，函数值随的增大而减小，求的取值范围；
以抛物线的顶点为一个顶点作该抛物线的内接正（，两点在抛物线上），请问：△的面积是与无关的定值吗？若是，请求出这个定值；若不是，请说明理由；
若抛物线与轴交点的横坐标均为整数，求整数的值．

若一次函数（是常数）与（是常数），满足且，则称这两函数是对称函数
当函数与是对称函数，求和的值；
在平面直角坐标系中，一次函数图象与轴交于点、与轴交于点，点与点 关于x轴对称，过点、的直线解析式是，求证：函数与是对称函数

二次函数中，自变量与函数的对应值如下表：

	…				1	2	3	4	…
	…								…

若，则一元二次方程的两个根的取值范围是
A.，               B.  ，
C. ，         D.  ，

如图，直线y=3x+3交轴于A点，交轴于B点，过A、B两点的抛物线交轴于另一点C（3，0）．（1）求抛物线的解析式；（2）求抛物线的对称轴和顶点坐标．

已知二次函数(均为常数，且)，若与的部分对应值如下表所示，则方程的根为                ．

下表是二次函数y = ax²+bx+c（a≠ 0）的变量x、y 的部分对应值：

x	…	-2	-1	0	1	2	…
y	…	4	6	6	4	0	…

则方程ax²+bx+c = 0的解是   .

如图，矩形在平面直角坐标系中的位置如图所示，，.抛物线（）经过点和点，与轴分别交于点、（点在点左侧），且，则下列结论：①；②；③；④；⑤连接、，则
，其中正确结论的个数为

A．个

B．个

C．个

D．个

如图，抛物线与两坐标轴的交点分别为（-1，0），（2，0），（0，2），则当时，自变量x的取值范围是（ ▲ ）

A．

B．

C．

D．