抛物线y=ax²+bx+c(a≠0)的对称轴是直线x=2,且经过点p(3‚0).则a+b+c的值为( )
| A.1 | B. 2 | C.–1 | D. 0 |
抛物线y=x2先向右平移1个单位,再向上平移3个单位,得到的抛物线解析式是
A. |
B. |
C. |
D. |
已知抛物线的顶点坐标为(2,9),且它在x轴上截得的线段长为6,则该抛物线的解析式为 .
如图,抛物线y=ax2与反比例函数 的图象交于P点,若P点横坐标为1,则关于x的不等式
的图象交于P点,若P点横坐标为1,则关于x的不等式 >0的解是( )
>0的解是( )
| A.x>1 | B.x<-1 | C.-1<x<0 | D.0<x<1 |

对于抛物线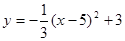 ,下列说法正确的是( )
,下列说法正确的是( )
| A.开口向下,顶点坐标是(5,3) | B.开口向上,顶点坐标是(5,3) |
| C.开口向下,顶点坐标是(-5,3) | D.开口向上,顶点坐标是(-5,3) |
市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: .设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
.设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
抛物线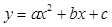 (a ≠ 0)满足条件:(1)
(a ≠ 0)满足条件:(1)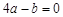 ;(2)
;(2)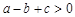 ;
;
(3)与x轴有两个交点,且两交点间的距离小于2.以下有四个结论:①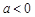 ;②
;②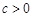 ;
;
③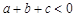 ;④
;④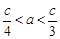 ,其中所有正确结论的序号是
,其中所有正确结论的序号是
若抛物线 的最低点的纵坐标为n,则m-n的值是( )
的最低点的纵坐标为n,则m-n的值是( )
A. |
B. |
C.1 | D.2 |