[浙江]2012届浙江省杭州市西湖区中考模拟(七)数学试卷
长为1,宽为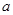 的矩形纸片(
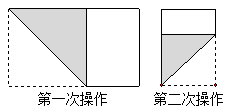
的矩形纸片(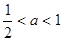 ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第
),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第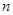 此操作后,剩下的矩形为正方形,则操作终止.当
此操作后,剩下的矩形为正方形,则操作终止.当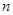 =3时,
=3时, 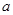 的值为_______.
的值为_______.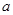
一根8cm长的尺子,只需刻上两个刻度就可以量出1—8之间的任何整数厘米长的物体长(“简称完全度量,分点分别为0、1、2、3、4、5、6、7、8)你觉的刻上两个刻度分别应该是 和 。
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点, CD=BD,∠C=70°,现给出以下四个结论:
① ∠A=45°;②AC=AB;③  弧AE=弧BE ; ④2CE·AB=BC2,
弧AE=弧BE ; ④2CE·AB=BC2,
其中正确结论的序号为 
用min{a,b}表示a,b两数中的最小值, 若函数y=min{|x|,|x+t|}的图象关于直线x=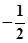 对称,则t的值为( )
对称,则t的值为( )
| A.-2 | B.2 | C.-1 | D.1 |
已知:a+b+c=3,a2+b2+c2=3,则a2011+b2011+c2011的值是 ( )
A 0 B 3 C 22005 D3·22005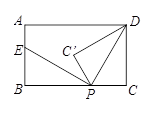
如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C 落到点C’处;作∠BPC’的角平分线交AB于点E.设BP=x,BE=y, 则下列图象中,能表示y与x的函数关系的图象大致是( )

如图,已知点A的坐标为( ,3),AB丄x轴,垂足为B,连接OA,反比例函数y=
,3),AB丄x轴,垂足为B,连接OA,反比例函数y=
(k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的 倍的长为半径作圆,则该圆与x轴的位置关系是( ).
倍的长为半径作圆,则该圆与x轴的位置关系是( ).
A.相离 B.相切 C.相交 D.以上都有可能
如图、在Rt△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
A. |
B. |
C. |
D. |

如图,在等腰Rt△ABC中斜边BC=9,从中裁剪内接正方形DEFG,其中DE在斜边BC上,点F、
G分别在直角边AC、AB上,按照同样的方式在余下的三角形中继续裁剪,如此操作下去,共可裁剪出边长
大于1的正方形( )个
A.2 B.3 C.4 D.5
已知a=( )
) ,b="2cos" 45
,b="2cos" 45 -
- ,c=(2011-
,c=(2011- )
) ,d=
,d=
(1)请化简这四个数;
(2) 从这四个数中任取两个,积为无理数的概率是多少。
如图,在平面直角坐标系中,过格点A,B,C作一圆弧,[
(1)在图中作出该弧的圆心O,则点O的坐标是( , );
(2)作出过点B且与该弧相切的直线;(原创)
如图,直线y=kx+b与反比例函数 只有一个交点A(1 , 2),且与x轴、y轴分别交于B,C两点,AD垂直平分OB,垂足为D,
只有一个交点A(1 , 2),且与x轴、y轴分别交于B,C两点,AD垂直平分OB,垂足为D,
(1)求点B的坐标和m的值;
(2)求直线解析式
某地区中考体育测试满分为40分,某九级进行了体育模拟测试,随机抽取了部分学生的考试成绩进行统计分析,并把分析结果绘制成如下两幅统计图、试根据统计图中提供的数据,回答下列问题:
(1)抽取的样本中,成绩为39分的人数有 人;
(2)抽取的样本中,考试成绩的中位数是 分,众数是 分;
(3)该地区体育考成绩39分以上(含39分)的为优秀,且要求优秀率不低于70%,
请通过计算说明本次体育模拟测试的优秀率是否达到要求?
某中学九年级甲、乙两班商定举行一次远足活动, 、
、 两地相距10千米,甲班从
两地相距10千米,甲班从 地出发匀速步行到
地出发匀速步行到 地,乙班从
地,乙班从 地出发匀速步行到
地出发匀速步行到 地.两班同时出发,相向而行.设步行时间为
地.两班同时出发,相向而行.设步行时间为 小时,甲、乙两班离
小时,甲、乙两班离 地的距离分别为
地的距离分别为 千米、
千米、 千米,
千米, 、
、 与
与 的函数关系图象如图所示,根据图象解答下列问题:
的函数关系图象如图所示,根据图象解答下列问题:
(1)直接写出 、
、 与
与 的函数关系式;
的函数关系式;
(2)求甲、乙两班学生出发后,几小时相遇?相遇时乙班离 地多少千米?
地多少千米?
(3)甲、乙两班相距4千米时所用时间是多少小时?
已知:以原点O为圆心,5为半径的半圆与y轴交于A、G两点,AB与半圆相切于点A,点B的坐标为(3, )。(如图1
)。(如图1 )过半圆上的点C
)过半圆上的点C 作y轴的垂线,垂足为D.Rt△DOC的面积为
作y轴的垂线,垂足为D.Rt△DOC的面积为 。
。
(1)求点C的坐标;
(2)①命题“如图2,以y轴为对称轴的等腰梯形MNPQ与M1N1P1Q1的上底和下底都分别在同一条直线上,NP∥MQ,PQ∥P1Q1,且NP>MQ.设抛物线y=a0x2+h0过点P、Q,抛物线y=a1x2+h1过点P1、Q1,则h0>h1”是真命题.请你以Q(3,5)、P(4,3)和Q1(p,5)、P1(p+1,3)为例进行验证;
②当图1中的线段BC在第一象限时,作线段BC关于y轴对称的线段FE,连接BF、CE,点T是线段BF上的动点(如图3);设K是过T、B、C三点的抛物线y=ax2+bx+c的顶点,求K的纵坐标yK的取值范围.
如图1,在直角梯形ABCD中,AD//BC,∠A=90°,AB=8cm,AD=6cm, BC=10cm。点P从点B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF从CD出发沿DA方向匀速运动,速度为1 cm/s,且EF与BD交于点Q,连接PE、PF。当点P与点Q相遇时,所有运动停止。若设运动时间为t(s).
(1)求CD的长度
(2)当PE//AB时,求t的值;
(3)①设△PEF的面积为S,求S关于t的函数关系式;
②如图2,当△PEF的外接圆圆心O恰好在EF中点时,则t的值为 (请直接写出答案)
 ,且
,且 ,则
,则 ________
________ 的值为正的条件是
的值为正的条件是  ,当
,当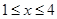 时,则函数
时,则函数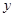 的取值范围是_ ___
的取值范围是_ ___ 的平方根是 ( )
的平方根是 ( ) B ±
B ± D ±
D ± 与
与 的平均数是6,那么
的平均数是6,那么 与
与 的平均数是( )
的平均数是( )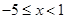 是( )。
是( )。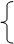

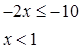 C.
C. 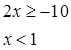 D.
D. 
 的最低点的纵坐标为n,则m-n的值是( )
的最低点的纵坐标为n,则m-n的值是( )

 粤公网安备 44130202000953号
粤公网安备 44130202000953号