[浙江]2012届浙江省台州地区九年级第二学期七校联考数学试卷
如图,日食图中表示太阳和月亮的分别为两个圆,这两圆的位置关系是( ).
A.外离 B.相交 C.外切 D.内含 
对于抛物线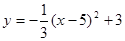 ,下列说法正确的是( )
,下列说法正确的是( )
| A.开口向下,顶点坐标是(5,3) | B.开口向上,顶点坐标是(5,3) |
| C.开口向下,顶点坐标是(-5,3) | D.开口向上,顶点坐标是(-5,3) |
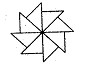
右图可以看作是由一个等腰直角三角形旋转若干次而生成的, 则每次旋转的度数至少是( )
| A.900 | B.600 | C.450 | D.300 |
下列说法正确的是( )
| A.打开电视看CCTV—5频道,正在播放NBA篮球比赛是必然事件 |
| B.某一种彩票中奖概率是,那么买1000张这种彩票就一定能中奖 |
| C.度量一个三角形的内角和是360°,这是不可能事件 |
| D.小李掷一硬币,连续5次正面朝上,则他第6次掷硬币时,正面朝上的概率是1 |
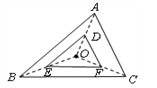
如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
A. |
B.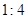 |
C.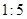 |
D. |
已知二次函数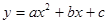 的
的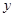 与
与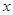 的部分对应值如下表:
的部分对应值如下表:
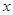 |
… |
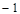 |
0 |
2 |
4 |
… |
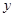 |
… |
-2 |
1 |
3 |
1 |
… |
则下列判断①当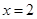 时,函数取得最大值3;②
时,函数取得最大值3;②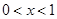 时,函数
时,函数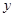 随
随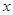 的增大而增大;③a+b+c<0;④存在
的增大而增大;③a+b+c<0;④存在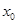 满足
满足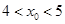 ,当
,当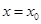 时,函数值为0.其中不正确的结论有( )
时,函数值为0.其中不正确的结论有( )
A.1个 B.2个 C.3个 D.4个
在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型(如图),它的底面半径 高
高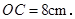 则这个圆锥漏斗的侧面积是 .
则这个圆锥漏斗的侧面积是 .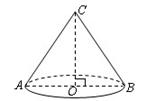
某种商品在两个月内降价两次,现在该商品每件的价格比两个月前下降了36%,问
平均每月降价百分之几?设平均每月降价的百分率为x,则可列方程为 .
已知A、B、C、D点的坐标如图所示,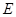 在线段AC的延长线上, 若△ABC 和△ADE相似, 则
在线段AC的延长线上, 若△ABC 和△ADE相似, 则 点的坐标是___________________.
点的坐标是___________________. 
已知关于x的方程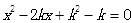 .
.
(1)当方程有两个不相等的实数根时,求k的取值范围;
(2)当方程的一个根是2时,求k的值.
如图,在平面直角坐标系中,已知点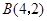 ,
,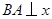 轴于A.将点B绕原点逆时针旋转90°后记作点
轴于A.将点B绕原点逆时针旋转90°后记作点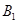 ,作出旋转后的
,作出旋转后的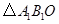 .
.
(1)点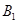 的坐标为 ;
的坐标为 ;
(2)求点B所经过的路径长.
某商场开展购物抽奖活动,抽奖箱中有3个形状、大小和质地等完全相同的小球,分别标有数字1、2、3.顾客从中随机摸出一个小球,然后放回箱中,再随机摸出一个小球.
(1)利用树形图法或列表法(只选其中一种),表示摸出小球可能出现的所有结果;
(2)若规定:两次摸出的小球的数字之积为9,则为一等奖;数字之积为偶数,则为二等奖.请你分别求出顾客抽中一等奖、二等奖的概率.
如图,BD是⊙O的直径,过点D的切线交⊙O的弦BC的延长线于点E,弦AC∥DE交BD于点G
(1)求证:BD平分弦AC;
(2)若弦AD=5㎝,AC=8㎝,求⊙O的半径.
某大学毕业生,投资开办了一个装饰品商店.该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30,且x为整数);又知这30天的销售价格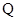 (元/件)与销售时间x(天)之间有如下关系:
(元/件)与销售时间x(天)之间有如下关系: (1≤x≤30,且x为整数).
(1≤x≤30,且x为整数).
(1)试写出该商店这30天的日销售利润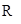 (元)与销售时间x(天)之间的函数关系式;
(元)与销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润达到896元且日销售量较大?(注:销售利润=销售收入一购进成本)
阅读理解:如图1,在直角梯形ABCD中,AB∥CD,∠B=900,点P在BC边上,当
∠APD=900时,易证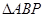 ∽
∽ ,从而得到
,从而得到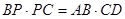 ,解答下列问题.
,解答下列问题.
(1)模型探究1:如图2,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时, 结论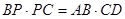 仍成立吗? 试说明理由;
仍成立吗? 试说明理由;
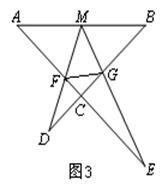
(2)拓展应用:如图3,M为AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°且DM交AC于F,ME交BC于G.AB=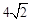 ,AF=3,求FG的长.
,AF=3,求FG的长.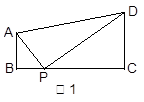
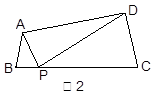
如图1,矩形 ,
,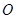 为原点,点
为原点,点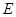 在
在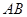 上,把
上,把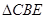 沿
沿 折叠,使点
折叠,使点 落在
落在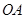 边上的点
边上的点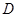 处,A、D坐标分别为
处,A、D坐标分别为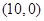 和
和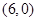 ,抛物线
,抛物线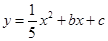 过点
过点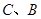 .
.
(1)求 点的坐标及该抛物线的解析式;
点的坐标及该抛物线的解析式;
(2)如图2,矩形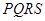 的长、宽一定,点
的长、宽一定,点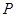 沿(1)中的抛物线滑动,在滑动过程中
沿(1)中的抛物线滑动,在滑动过程中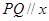 轴,且
轴,且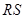 在
在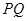 的下方,当
的下方,当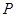 点横坐标为-1时,点
点横坐标为-1时,点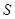 位于
位于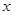 轴上方且距离
轴上方且距离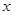 轴
轴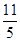 个单位.当矩形
个单位.当矩形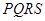 在滑动过程中被
在滑动过程中被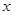 轴分成上下两部分的面积比为2:3时,求点
轴分成上下两部分的面积比为2:3时,求点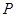 的坐标;
的坐标;
(3)如图3,动点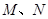 同时从点
同时从点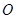 出发,点
出发,点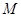 以每秒3个单位长度的速度沿线段
以每秒3个单位长度的速度沿线段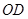 运动,点
运动,点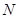 以每秒8个单位长度的速度沿折线
以每秒8个单位长度的速度沿折线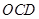 按
按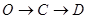 的路线运动,当
的路线运动,当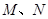 中的其中一点停止运动时,另一点也停止运动.设
中的其中一点停止运动时,另一点也停止运动.设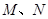 同时从点
同时从点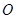 出发秒时,
出发秒时,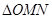 的面积为
的面积为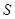 .求
.求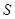 与的函数关系式,并写出的取值范围.
与的函数关系式,并写出的取值范围.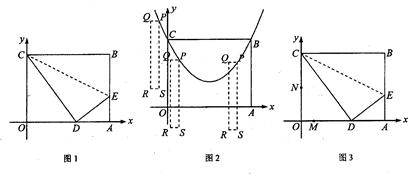

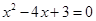 时可配方得( )
时可配方得( )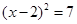
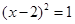
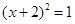
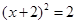
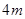 的正六边形,则地基的周长是( )
的正六边形,则地基的周长是( )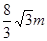
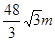
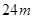
 在实数范围内有意义.
在实数范围内有意义.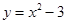 向上平移一个单位后,得到的新抛物线的表达式是 .
向上平移一个单位后,得到的新抛物线的表达式是 .
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号