[广东]2012年初中毕业升学考试(广东深圳卷)数学
第八届中国(深圳)文博会以总成交额143 300 000 000元再创新高.将数143 300 000 000用科学记数法表示为【 】
A, B。
B。 C。
C。 D。
D。
体育课上,某班两名同学分别进行5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的【 】
| A.平均数 | B.频数分布 | C.中位数 | D.方差 |
如图所示,一个60o角的三角形纸片,剪去这个600角后,得到 一个四边形,则么 的度数为【 】
的度数为【 】
| A.120O | B.180O. | C.240O | D.3000 |
端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽、3只碱水粽、5只咸肉粽,粽子除内部馅料不同外其它均相同.小颖任意吃一个,吃到红豆粽的概率是【 】
A. |
B. |
C. |
D. |
下列命题
①方程x2=x的解是x=1
②4的平方根是2
③有两边和一角相等的两个三角形全等
④连接任意四边形各边中点的四边形是平行四边形
其中真命题有:【 】
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内 上一点,∠BM0=120o,则⊙C的半径长为【 】
上一点,∠BM0=120o,则⊙C的半径长为【 】
A.6 B.5 C.3 D。
小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300,同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为【 】
A. 米 米 |
B.12米 | C. 米 米 |
D.10米 |
如图,已知:∠MON=30o,点A1、A2、A3在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7的边长为【 】
| A.6 | B.12 | C.32 | D.64 |
如图,双曲线 与⊙O在第一象限内交于P、Q 两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为 ▲ .
与⊙O在第一象限内交于P、Q 两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为 ▲ .
)如图,Rt△ABC中,C= 90o,以斜边AB为边向外作正方形 ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6 ,则另一直角边BC的长为 ▲ .
,则另一直角边BC的长为 ▲ .
为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:
| 分数段 |
频数 |
频率 |
| 60≤x<70 |
30 |
0.1 |
| 70≤x<80 |
90 |
n |
| 80≤x<90 |
m |
0.4 |
| 90≤x≤100 |
60 |
0.2 |

请根据以上图表提供的信息,解答下列问题:
(1)本次调查的样本容量为
(2)在表中:m= .n= ;
(3)补全频数分布直方图:
(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在
分数段内;
(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.
(1)求证:四边形AFCE为菱形;
(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.
“节能环保,低碳生活”是我们倡导的一种 生活方式,某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台,三种家电的进价和售价如下表所示: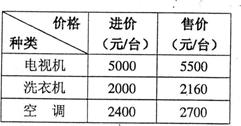
(1)在不超出现有资金前提下,若购进电视机的数量和洗衣机的数量相同,空调的数量不超过电视机的数量的3倍.请问商场有哪几种进货方案?
(2)在“2012年消费促进月”促销活动期问,商家针对这三种节能型)品推出“现金每购满1000元送50元家电消费券一张、多买多送”的活动.在(1)的条件下若三种电器在活动期间全部售出,商家预估最多送出消费券多少张?
如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).
(1)求经过A、B、C三点的抛物线解析式;
(2)设直线BC交y轴于点E,连接AE,求证:AE=CE;
(3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F,为顶点的三角形与△ABC相似吗?
请说明理由.



 B。
B。 C。
C。 D。
D。




 ▲
▲  的最小值是 ▲ .
的最小值是 ▲ .
 = -3,
= -3, =2,求代数式
=2,求代数式 的值.
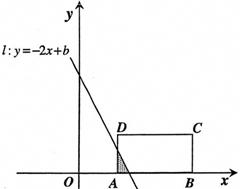
的值. :y=-2x+b (b≥0)的位置随b的不同取值而变化.
:y=-2x+b (b≥0)的位置随b的不同取值而变化.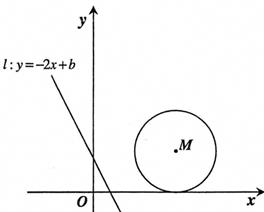
 粤公网安备 44130202000953号
粤公网安备 44130202000953号