初中数学一元二次方程的最值试题

已知三角形的两边长是方程x ²－5x＋6=0的两个根，则该三角形的周长的取值范围是．

阅读下列例题：
解方程x²-|x|-2=0
解：（1）当x≥0时，原方程化为x²-x-2=0，解得x₁=2，x₂=-1（舍去）．
当x＜0时，原方程化为x²+x-2=0，解得x₁=1（舍去），x₂=-2．
∴x₁=2，x₂=-2是原方程的根．
请参照例题解方程：x²-|x-1|-1=0．

为满足市场需求，某超市在中秋节来临前夕，购进一种品牌月饼，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出1600盒，每盒售价每提高1元，每天要少卖出20盒．
（1）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？
（2）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得6000元的利润，那么超市每天销售月饼多少盒？

关于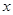的一元二次方程.
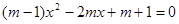（1）求证：方程有两个不相等的实数根；
（2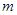）为何整数时，此方程的两个根都为正整数．

已知关于x的一元二次方程。
（1）求证：方程有两个不相等的实数根；
（2）若△ABC的两边AB、AC的长是方程的两个实数根，第三边BC的长为5。当△ABC是等腰三角形时，求k的值。

实数x满足方程（x²+x）²-（x²+x）-2=0，则x²+x的值等于（）

A．2

B．

C．2或

D．1或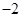

关于x的方程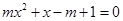，有以下三个结论：①当m=0时，方程只有一个实数解②当时，方程有两个不等的实数解③无论m取何值，方程都有一个负数解，其中正确的是（填序号）

20．解方程：
（1）解方程：x²-6x-2=0；
（2）．

已知关于x的一元二次方程．
（1）若此方程有两个不相等的实数根，求实数k的取值范围；
（2）已知x=3是此方程的一个根，求方程的另一个根及k的值；
（3）当Rt△ABC的斜边长C=，且两条直角边A和B恰好是这个方程的两个根时，求Rt△ABC的面积．

某商场将某种商品的售价从原来的每件40元经两次调价后调至每件32.4元．
（1）若该商店两次调价的降价率相同，求这个降价率；
（2）经调查，该商品每降价0.2元，即可多销售10件．若该商品原来每月可销售500件，那么两次调价后，每月可销售该商品多少件？

如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB），且OA、OB的长分别是一元二次方程x²-（＋1）x＋＝0的两个根．点C在x轴负半轴上，且AB：AC＝1：2．

（1）求A、C两点的坐标．
（2）若点M从点C出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围．
（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，说明理由．

对x，y定义一种新运算T，规定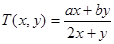：（其中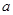、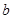均为非零常数），这里等式右边是通常的四则运算，例如：．
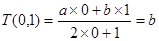（1）已知T（1，﹣1）=﹣2，T（4，2）=1．
①求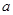、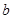的值；
②若关于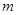的方程T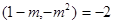有实数解，求实数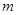的值；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则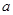、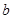应满足怎样的关系式？

解方程：
（1）x（x-2）=x-2；
（2）（x+8）（x+1）=-12．

已知关于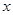的一元二次方程x²－4x＋k＋1＝0
（1）若=－1是方程的一个根，求k值和方程的另一根；
（2）设x₁，x₂是关于x的方程x²－4x＋k＋1＝0的两个实数根，是否存在实数k，使得x₁x₂＞x₁＋x₂成立？请说明理由．

佳佳超市经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，出售价格每涨价1元，日销售量将减少20千克，现佳佳超市要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？