初中数学一元二次方程的最值试题

（本小题满分8分）新华商场销售某种空调，每台进货价为2500元．市场调研表明：当销售价为2900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台．商场要想使这种空调的销售利润平均每天达到5000元，每台空调的定价应为多少元？

某超市经销一种成本为40元/kg的水产品，市场调查发现，按50元/kg销售，一个月能售出500kg，若每千克每涨1元，月销售量就减少10kg，针对这种水产品的销情况，超市在月成本不超过10000元的情况下，使得月销售利润达到8000元，请你帮忙算算，销售单价定为多少元？

使分式的值等于零的x是（）

A．6

B．﹣1或6

C．﹣1

D．﹣6

（1）已知一元二次方程的两根为，求证，．
（2）已知关于x的一元二次方程的两个不相等实数根满足，求a的值．
（3）已知抛物线与x轴交于A．B两点，且过点（-1，-1），设线段AB的长为d，当p为何值时，取得最小值，并求出最小值．

我县某楼盘准备以每平方米4000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米3240元的均价开盘销售．
（1）求平均每次下调的百分率．
（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9．8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？

阅读下列例题：
解方程x²-|x|-2=0
解：（1）当x≥0时，原方程化为x²-x-2=0，解得x₁=2，x₂=-1（舍去）．
当x＜0时，原方程化为x²+x-2=0，解得x₁=1（舍去），x₂=-2．
∴x₁=2，x₂=-2是原方程的根．
请参照例题解方程：x²-|x-1|-1=0．

已知，如图：四边形ABCD中，∠C＞90°，CD⊥AD于D，CB⊥AB于B，AB=，tanA是关于x的方程的一个实数根。

（1）求tanA；
（2）若CD=m，求BC的值。

某超市经销一种成本为40元/的水产品，市场调查发现，按50元/销售，一个月能售出500，销售单价每涨1元，月销售量就减少10，针对这种水产品的销售情况，超市在月成本不超过10000元的情况下，使得月销售利润达到8000元，请你帮忙算算，销售单价定为多少？

如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB），且OA、OB的长分别是一元二次方程x²-（＋1）x＋＝0的两个根．点C在x轴负半轴上，且AB：AC＝1：2．

（1）求A、C两点的坐标．
（2）若点M从点C出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围．
（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，说明理由．

某超市销售一种旅游纪念品，平均每天可售出20套，每套盈利40元．“十一”期间，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存．经市场调查发现：如果每套降价1元，那么平均每天就可多售出2套．要想平均每天销售这种纪念品盈利1200元，那么每套应降价多少元？

解方程：
（1）x（x-2）=x-2；
（2）（x+8）（x+1）=-12．

某商场将某种商品的售价从原来的每件40元经两次调价后调至每件32.4元．
（1）若该商店两次调价的降价率相同，求这个降价率；
（2）经调查，该商品每降价0.2元，即可多销售10件．若该商品原来每月可销售500件，那么两次调价后，每月可销售该商品多少件？

解方程
（1）x²－10x=96
（2）阅读下面的例题：
解方程x²-|x|－2=0．
解：分两种情况讨论：
①当x≥0时，原方程化为x²－x－2=0．
解得：x₁=2，x₂=－1(不合题意，舍去)；
②当x＜0时，原方程化为x²＋x－2=0．
解得：x₁=－2，x₂=1(不合题意，舍去)；
综上所述，原方程的根是x₁=2，x₂=－2．
请参照前面的例题的解法解方程：x²-|x－1|－1=0

已知关于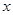的一元二次方程x²－4x＋k＋1＝0
（1）若=－1是方程的一个根，求k值和方程的另一根；
（2）设x₁，x₂是关于x的方程x²－4x＋k＋1＝0的两个实数根，是否存在实数k，使得x₁x₂＞x₁＋x₂成立？请说明理由．

对x，y定义一种新运算T，规定：（其中、均为非零常数），这里等式右边是通常的四则运算，例如：．
（1）已知T（1，﹣1）=﹣2，T（4，2）=1．
①求、的值；
②若关于的方程T有实数解，求实数的值；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则、应满足怎样的关系式？