(1)解不等式:2(x+1)﹣1≥3x+2,并把解集表示在数轴上.
(2)解不等式组 ,并写出不等式组的整数解.
,并写出不等式组的整数解.
学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍;用600元单独购买甲种图书比单独购买乙种图书要少10本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书共40本,且投入的经费不超过1050元,要使购买的甲种图书数量 不少于乙种图书的数量,则共有几种购买方案?
某林场计划从外地购进两种小树苗2000棵进行栽培,已知甲种树苗每棵2元,乙种树苗每棵3元。
(1)若购买这批树苗共用4500元,求甲、乙两种树苗各购买了多少棵?
(2)若购买这批树苗的钱不超过4700元,问应选购甲种树苗至少多少棵?
(3)相关资料表明,甲、乙两种树苗的成活率分别是94%和99%,若要使这批树苗的成活率不低于96%,且树苗的总费用最少,问应选购甲、乙两种树苗各多少棵?总费用最少是多少元?
购进某种干果,由于销售状况良好,超市又用9000元第二次购进该干果,但第二次的进价比第一次的提髙了20%,第二次购进干果数量是第一次的2倍还多300千克.
(1)求该干果的第一次进价是每千克多少元?
(2)百姓超市按每千克9元的价格出售,当大部分干果售出后,余下的按售价的8折售完,若两次销售这种干果的利润不少于5820元,则最多余下多少千克干果按售价的8折销售.
“保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2) 预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
已知关于x的方程4x+2m+1=2x+5的解是负数.
(1)求m的取值范围;
(2)在(1)的条件下,解关于x的不等式2(x﹣2)>mx+3.
解不等式2(x+1)﹣1≥4x+3,并把它的解集在数轴上表示出来.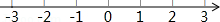
定义符号 的含义为:当
的含义为:当 时,
时, 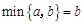 ;当
;当 时,
时,  .如:
.如: ,
, .
.
(1)求 ;
;
(2)已知 , 求实数
, 求实数 的取值范围;
的取值范围;
(3)当 时,
时, .直接写出实数
.直接写出实数 的取值范围.
的取值范围.