初中数学含绝对值的一元一次不等式试题

不等式组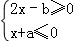的解集为3≤x≤6，则不等式ax+b＜0的解集为      ．

解下列不等式组，并将解集在数轴上表示出来。

（1997•河北）由x＜y得到ax＞ay的条件是（ ）

A．a≥0

B．a≤0

C．a＞0

D．a＜0

已知不等式组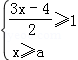的解集是x≥2，则（ ）

A．a＜2

B．a=2

C．a＞2

D．a≤2

若a＜2，则关于x的不等式ax＞2x+a﹣2的解集为            ．

关于x的不等式组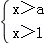的解集为x＞1，则a的取值范围是（ ）

A．a≥1

B．a＞1

C．a≤1

D．a＜1

不等式（3x+4）（3x﹣4）＜9（x﹣2）（x+3）的最小整数解为      ．

解不等式组．

解下列不等式（组）
（1） 
（2）

某校为了奖励在数学竞赛中获奖的学生，买了若干本课外读物准备奖励给他们，如果每人奖4本，则剩余8本；如果每人奖5本，则最后一人得到了课外读物但不足3本．设该校买了本课外读物，有x名学生获奖．
（1）用含x的代数式表示y；
（2）求出该校的获奖人数及所买课外读物的本数．

已知关于x的方程4x+2m+1=2x+5的解是负数．
（1）求m的取值范围；
（2）在（1）的条件下，解关于x的不等式2（x﹣2）＞mx+3．

已知方程组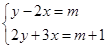的解x、y满足2x+y≥0，则m的取值范围是（   ）

A．m≥—

B．m≥

C．m≥1

D．—≤m≤1

解不等式2（x+1）﹣1≥4x+3，并把它的解集在数轴上表示出来．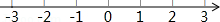

解不等式（组），并把解集在数轴上表示出来．
（1）
（2）．

小武新家装修，在装修客厅时，购进彩色地砖和单色地砖共100块，共花费5600元．已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块．
（1）两种型号的地砖各采购了多少块？
（2）如果厨房也要铺设这两种型号的地砖共60块，且采购地砖的费用不超过3200元，那么彩色地砖最多能采购多少块？