初中数学含绝对值的一元一次不等式试题

如果不等式组无解，那么m的取值范围是（    ）

A．

B．

C．

D．

不等式组 的最小整数解是（    ）

A．0

B．－1

C．1

D．2

解不等式组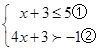请结合题意填空，完成本题的解答：
（1）解不等式①，得     ；
（2）解不等式②，得       ；
（3）把不等式①和②的解集在数轴上表示出来：       ．
（4）原不等式组的解集为       ．

解不等式组

已知，，当          时，．

不等式（3x+4）（3x﹣4）＜9（x﹣2）（x+3）的最小整数解为      ．

（满分8分）某校运动会需购买A、B两种奖品．若购买A种奖品3件和B种奖品2件，共需60元；若购买A种奖品5件和B种奖品3件，共需95元．
（1）求A、B两种奖品单价各是多少元？
（2）学校计划购买A、B两种奖品共100件，购买费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍．设购买A种奖品m件，购买费用为W元，写出W（元）与m（件）之间的函数关系式，求出自变量m的取值范围，并确定最少费用W的值．

x的3倍与8的和比y的2倍小，用不等式表示数量关系             ．

若＞，则下列不等式成立的是（    ）

A．＜

B．＞

C．＜

D．＞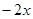

已知关于x的方程4x+2m+1=2x+5的解是负数．
（1）求m的取值范围；
（2）在（1）的条件下，解关于x的不等式2（x﹣2）＞mx+3．

解不等式2（x+1）﹣1≥4x+3，并把它的解集在数轴上表示出来．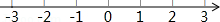

解不等式（组），并把解集在数轴上表示出来．
（1）
（2）．

小武新家装修，在装修客厅时，购进彩色地砖和单色地砖共100块，共花费5600元．已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块．
（1）两种型号的地砖各采购了多少块？
（2）如果厨房也要铺设这两种型号的地砖共60块，且采购地砖的费用不超过3200元，那么彩色地砖最多能采购多少块？

若一个三角形的三边长分别是xcm、(x+4)cm、(12-2x)cm，则x的取值范围是         ．

若成立，则下列不等式成立的是（   ）

A．	B．
C．	D．