先阅读下列材料,再解答后面的问题:
要求算式 的值,我们可以按照如下方法进行:
的值,我们可以按照如下方法进行:
设 =S ① 则有2(
=S ① 则有2( )= 2S
)= 2S
∴  = 2S ②
= 2S ②
②-①得: = S ∴
= S ∴  = S
= S
∴ 原式:  =
= 
㈠ 请你根据上述方法计算:  = 。
= 。
㈡ 2008年美国的金融危机引发了波及全世界的经济危机,我国也在此次经济危机中深受影响,为此2009年我国积极理性的放宽信贷,帮助我国企业、特别是中小企业度过难关,尽最大努力减少我国的失业率。 某企业在应对此次危机时积极进取,决定贷款进行技术改造,现有两种方案, 甲方案: 一次性贷款10万元,第一年便可获利1万元,以后每年获利比前一年增加30%的利润;
乙方案: 每年贷款1万元,第一年可获利1万元,以后每年获利比前一年增加5千元;
两种方案的使用期都是10年,到期一次性归还本息. 若银行两种形式的贷款都按年息5%的复利计算,
试比较两种方案中,10年的总利润,哪种获利更多? ( 结果精确到0.01 )
(取1.0510 =" 1.629" , 1.310 =" 13.786" , 1.510 =" 57.665" )
( 注意:‘复利’的计算方法,例如:一次性贷款7万元,按年息5%的复利计算;⑴若1年后归还本息,则要还 元。⑵若2年后归还本息,则要还
元。⑵若2年后归还本息,则要还 元。⑶若3年后归还本息,则要还
元。⑶若3年后归还本息,则要还 元。 )
元。 )
阅读下列材料,并解答后面的问题:
∵ =
= (1-
(1- ),
),  =
= (
( -
- ), … ,
), … , =
= (
( -
- )
)
∴ ……+
……+
= (1-
(1- )+
)+ -
- )+ … +
)+ … + -
- )
)
=
=
=
①在式子 中,第五项为 ,第n项为 。
中,第五项为 ,第n项为 。
②解方程: =
= (有计算过程)
(有计算过程)
小花猫从某点O出发在一直线上来回跑动,假定向右跑的路程记为正,向左跑的路程记为负,跑动的各段路程依次为(单位:m)
+4,-2,+5,-7,-6,+9,-5,+12
(1)问:小花猫最后在出发点的哪一边?离开出发点O相距多少?
(2)在跑动过程中,如果每跑过10米奖励一条小鱼,则小花猫一共得到多少条小鱼?
阅读理解并解答:(本题3分)
为了求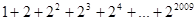 的值,可令
的值,可令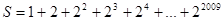 ,
,
则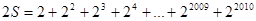 , 因此
, 因此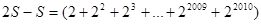 -
-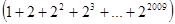 =
=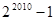 。
。
所以: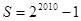 。即
。即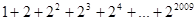 =
=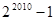 。
。
请依照此法,求: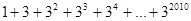 的值。
的值。
个体户小李花141000(含十年经营权)购买了一辆出租车,平均每月营运收入9200元,平均每月支出各种费用4500元。
(1)他几个月后开始赢利?
(2)若出租车营运期限为10年(即10年后,只能折旧,卖车,不能再营运),到期后预计旧车可卖0.3万元。问这车10年内的年平均赢利多少元?
某出租车一天下午以A点为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位: )依先后次序记录如下:
)依先后次序记录如下: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.将最后一名乘客送到目的地,出租车离出发地点A多远?在点A的什么方向?
若每千米的价格为2.4元,司机一个下午的营业额是多少?
如图,从顶点A出发,沿着边长为1的正方形的四个顶点依次跳舞,舞步长为1.第一次顺时针移动1步,第二次逆时针移动2步,第三次顺时针移动3步,……以此类推.
(1)移动4次后到达何处?(直接给出答案)
(2)移动2012次后到达何处?