[江西]2011-2012学年江西九江七年级第二学期期中联考数学试卷
某红外线遥控器发出的红外线波长为0.000 000 94m,用科学记数法表示这个数是( )
A.9.4×108m B.9.4×107m C.9.4×10-8m D.9.4×10-7 m
下列各式中,不能用平方差公式计算的是( )
| A.(-x+y)(-x-y) | B.(x-y)(-x+y) | C.(-x-y)(x-y) | D.(x+y)(-x+y) |
对于四舍五入得到的近似数5.00×104,下列说法正确的是( )
| A.有3个有效数字,精确到百分位 | B.有1个有效数字,精确到百分位 |
| C.有3个有效数字,精确到百位 | D.有1个有效数字,精确到万位 |
已知三条不同的直线a,b,c在同一平面内,下列说法正确的个数是( )
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
A,1个 B.2个 C.3个 D.4个
某食堂六月份1日至5日每天用水量变化情况如图所示,那么在这5天内,最多一天的用水量与最少一天的用水量差是 吨.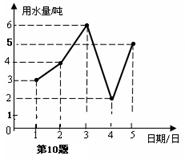
如图,有一块含30°角的直角三角板(∠A=30°,∠C= 90°)的一个顶点放在直尺的一边上,若∠1=20°.那么∠2的度数是 .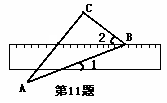
将一些相同的小三角形按下图所示的规律摆放,请仔细观察,第 n个图形有 个小三角形.(用含 n 的代数式表示)
某校准备召开一次学生代表会,七(1)班有5个参会名额,其中男生必须有m人,于是七(1)班班主任确定从9名(5男4女,其中班长吴英为女生)候选人员中选取.若“选到吴英”的可能性是大于0但小于1,则m= .
(1)在图①正方形网格中,已知∠AOB及点E、F,现要求只用直尺,分别以E、F为顶点.画∠CEH、∠PFK,使∠CEH与∠AOB互余,且CE与OB互相垂直;使∠PFK与∠AOB互补,且FP∥OA,FK∥OB.
(2)在图②中,已知∠AOB,点E在OB上,请先用量角器画射线EC,使EC⊥EB于E,交OA于C,再用尺规作射线EH,使∠CEH与∠AOB互余,且EH∥OA.
(保留痕迹,不写作或画法,不说明理由).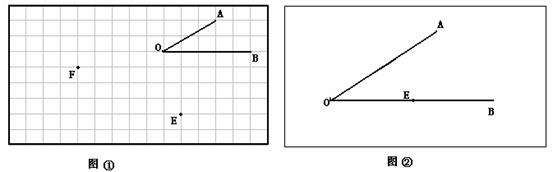
在同一副扑克中抽出了16张牌,其中红心有x张,方块有2x张,其他均为梅花,现将这16张牌洗匀背面朝下放在桌面上,A同学任意抽1张,若为红心则A同学获胜,A同学把抽出的牌放回并洗匀背面朝下放在桌面上,B同学再任意抽1张,若为梅花,则B同学获胜.
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
有这样一道题:“当 =0.302,
=0.302, =-0.239时,求(a+b)(a-b)+(4ab-8a2b2)÷4ab-a(a-2 b)多项式的值”,有一位同学指出题目中所给的条件“
=-0.239时,求(a+b)(a-b)+(4ab-8a2b2)÷4ab-a(a-2 b)多项式的值”,有一位同学指出题目中所给的条件“ =0.302,
=0.302, =-0.239”是多余的,问这位同学说的是否正确?若正确,请说明其理由;若不正确,多项式的值该是多少?
=-0.239”是多余的,问这位同学说的是否正确?若正确,请说明其理由;若不正确,多项式的值该是多少?
根据第五次、第六次全国人口普查结果显示:某市常住人口总数由第五次的400万人增加到第六次的450万人,常住人口的学历状况统计图如下(部分信息未给出):
解答下列问题:
(1)计算第六次人口普查小学学历的人数,并把条形统计图补充完整;
(2)第六次人口普查结果与第五次相比,该市常住人口中高中学历人数增长的百分比是多少?
如图,已知在△ 中,∠A=∠B
中,∠A=∠B 
(1)请你添加一个与直线AB有关的条件,由此可推得CE是∠ACD的角平分线(只添加条件,不说理由);
(2)请你添加一个与∠A有关的条件,由此可推得CE是∠ACD的角平分线. (要写出理由)
如图:某校一块长为2a米的正方形空地是七年级四个班的清洁区,其中分给七年级(1)班的清洁区是一块边长为(a-2b)米的正方形,(0<b< ),
),
(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米?
如图,在四边形纸片ABCD中,已知:AD∥BC,AB∥CD,∠B=90°,现将四边形纸片ABCD对折,折痕为PF(点P在BC上,点F在DC上),使顶点C落在四边形ABCD内一点C′,PC′的延长线交AD于M,再将纸片的另一部分对折(折痕为ME),使顶点A落在直线PM上一点A′.
(1)填空:
因为AD∥BC,(已知)
所以∠B+∠A=180°( )
又因为∠B=90°(已知)
所以∠A= 度.
则:∠EA′M= 度.
又因为AB∥CD(已知)
同理:∠FC′P=∠C= 度.
所以∠EA′M ∠FC′P(填 “<”或“=”或“>”)
所以 ∥ 理由:( ).
(2)ME与PF平行吗?请说明理由.








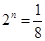 ,则n=
,则n= 
 中不含xy项.
中不含xy项.
 ,其中x=2.
,其中x=2. -2013×2011-1
-2013×2011-1 粤公网安备 44130202000953号
粤公网安备 44130202000953号