初中数学有理数无理数的概念与运算填空题

的相反数是        ，绝对值是        ，倒数是        .

在下列几个说法中，错误的个数是           个
（1）一个数，如果不是正数，必定就是负数；
（2）－a是负数；
（3）若两个数的积为1，则这两个数互为倒数；
（4）一个数的相反数是本身，则这个数一定是0；
（5）若两个数的绝对值相等，则这两个数也相等。

如图，对于大于或等于2的自然数n的平方进行如下“分裂”，分裂成n个连续奇数的和，则自然数9²的分裂数中最大的数是              ．

如图，按此规律，第6行最后一个数字是         ，第         行最后一个数是2014．

（本题4分）把下列各数分别填入相应的集合内：
－2．5，0，8，－2，，，－0．5252252225…（每两加1个2）．
（1）正数集合：｛                …｝；
（2）负数集合：｛                 …｝；
（3）整数集合：｛                …｝；
（4）无理数集合：{                …}．

将自然数从1开始按如图所示的规律进行排列，那么按这样的规律排列下去，2015应该在第        列。

用“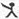”、“”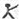定义新运算：对于任意实数a，b，都有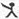ab=a和a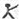b=b，例如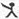32=3，3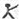2=2。则（2013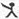2014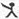） （20112012）的值是            

（1）如图，圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五个点按顺时针方向依次编号为1，2，3，4，5，若从某一点开始，沿圆周顺时针方向行走，点的编号是数字几，就走几段弧长，则称这种走法为一次“移位”．如：小明在编号为3的点，那么他应走3段弧长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的点，然后从1→2为第二次“移位”．小明从编号为4的点开始，第三次“移位”后，他到达编号为    的点，第2012次“移位”后，他到达编号为     的点．

（2）若将圆进行二十等份，按照顺时针方向依次编号为1，2，3，…，20，小明从编号为3的点开始，沿顺时针方向，按上述“移位”方式行走，
①经过4次“移位”后，他到达编号为        的点．
②“移位”次数a=      时，小王刚好到达编号为16的点，又满足|a-2012|的值最小．

用“☆”“★”定义新运算；对于任意实数a、b，都有a☆b＝a和a★b＝b．例如5☆2＝5，2★4＝4，则2014☆(2014★2015)＝_______。

已知，则的值是        ．

某初中校为每个学生编号，设定末尾用1表示男生，用2表示女生，若201103202表示“2011年入学的3班20号同学，是位女生”，则2012年入学的5班13号男生的编号是　　．

如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下次沿顺时针方向跳两个点；若停在偶数点上，则下次沿逆时针方向跳一个点．若青蛙从5这点开始跳，则经过2013次后它停在哪个数对应的点上               .

直线上有2014个点，我们进行如下操作：在每相邻两点间插入1个点，经过3次这样的操作后，直线上共有             个点．

式子“”表示从1开始的100个连续自然数的和，由于上述式子比较长，书写也不方便，为了简便起见，我们可以将“”表示为，这里的符号“”是求和的符号，如“”即从1开始的100以内的连续奇数的和，可表示为．通过对以上材料的阅读，请计算： （填写最后计算结果）．

把数字按如图所示排列起来，从上开始，依次为第一行、第二行、第三行……，中间用虚线围的一列，从上至下依次为1、5、13、25、…，则第10个数为                    。