小虫从某点O出发在一直线上来回爬行，假定向右爬行的路程记整数为正数，向左爬行的路程记为负数，爬行的各段路程依次为（单位：cm）：+5，－3，+10，－8，－6，+12，－10.
求：⑴小虫最后是否回到出发点O？
⑵ 小虫离出发点O最远是多少厘米？
⑶ 在爬行过程中，如果每爬行1厘米奖励一粒芝麻，则小虫一共得到多少粒芝麻？
请把下列各数填入相应的集合中
， 5.2， 0， 
， 
， 
,
，2005 , -0.030030003…
正数集合：｛ …｝分数集合：｛ …｝
非负整数集合：｛ …｝有理数集合：｛ …｝
从2开始，连续的偶数相加，它们的和的情况如下表：
加数m的个数 和(S)
1 ———————————→2＝1×2
2 ————————→2＋4＝6＝2×3
3 ——————→2＋4＋6＝12＝3×4
4 ————→2＋4＋6＋8＝20＝4×5
5 ——→2＋4＋6＋8＋10＝30＝5×6
(1)按这个规律，当m＝6时，和为_______；
(2)从2开始，m个连续偶数相加，它们的和S与m之间的关系，用公式表示出来为：
__________________________________________．
(3)应用上述公式计算：
①2＋4＋6＋…＋200 ②202＋204＋206＋…＋300
已知A、B在数轴上分别表示a，b．
(1)对照数轴填写下表：
(2)若A、B两点间的距离记为d，试问：d和a，b有何数量关系?
(3)在数轴上标出所有符合条件的整数点P，使它到10和－10的距离之和为20，并求所有这些整数的和；
(4)找出(3)中满足到10和－10的距离之差大于1而小于5的整数的点P；
(5)若点C表示的数为x，当点C在什么位置时，
取得的值最小?
根据某地实验测得的数据表明，高度每增加1 km，气温大约下降6℃，已知该地地面温度为21℃．
(1)高空某处高度是8 km，求此处的温度是多少；
(2)高空某处温度为一24 ℃，求此处的高度．
2009年3月17日俄罗斯特技飞行队在名胜风景旅游区——张家界天门洞特技表演，其中一架飞机起飞后的高度变化如下表：
(1)此时这架飞机比起飞点高了多少千米？
(2)如果飞机每上升或下降1 km需消耗2L燃油，那么这架飞机在这4个动作表演过程中，一共消耗了多少升燃油？
(3)如果飞机做特技表演时，有4个规定动作，前3个动作起飞后高度变化如下：上升3.8km，下降2.9km，再上升1.6km,若要使飞机最终比起飞点高出1km，问第4个动作是上升还是下降，上升或下降多少千米？
把下列各数化简后在数轴上表示出来，并把它们按从小到大的顺序用“＜”号连接起来。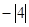
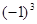
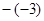
有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
(1)20筐白菜中，最重的一筐比最轻的一筐重多少千克？ (2分)
(2)与标准重量比较，20筐白菜总计超过或不足多少千克？
(3)若白菜每千克售价0.7元，则出售这20筐白菜可卖多少元？(2 分)
若“⊙”表示一种新运算，它的意义是：a⊙b=ab-(a+b),请计算下列格式的值。（1）（-3）⊙5 ； （2）2⊙ (共5分)
有20筐白菜，以每筐25千克为标准，超过或不足的分别用正、负来表示，记录如下：
| 与标准质量的差（单位：千克） |
－3 |
－2 |
－1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
2 |
8 |
（1）20筐白菜中，最重的一筐比最轻的一筐要重多少千克？
（2）与标准质量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2.6元，则出售这20筐白菜可卖多少元？
，
，
….
× ，
× .
…
，
，
，
，0，
，
.
”号把各数从小到大连起来：
。
，若
， 
，则
，
， 
， 
，
粤公网安备 44130202000953号