某汽车销售公司一位销售经理月份的汽车销售统计图如下:
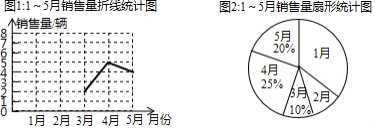
(1)已知1月的销售量是2月的销售量的3.5倍,则1月的销售量为 辆.在图2中,2月的销售量所对应的扇形的圆心角大小为 .
(2)补全图1中销售量折线统计图.
(3)已知4月份销售的车中有3辆国产车和2辆合资车,国产车分别用、
、
表示,合资车分别用
、
表示,现从这5辆车中随机抽取两辆车参加公司的回馈活动,请用列举法(画树状图或列表)求出“抽到的两辆车都是国产车“的概率.
某校开展了“我爱古诗词”知识竞赛活动,将某年级参赛学生的成绩划分为三个等级进行统计分析,绘制得到如图表.
成绩等级 |
频数 |
频率 |
75 |
||
0.4 |
||
105 |
0.35 |
请结合图表信息,解答下列问题:
(1)该年级学生共有多少人?
(2)求表中,
的值,并补全条形统计图;
(3)学校决定从参赛的甲、乙、丙、丁四名同学中任意抽取两名同学做经验介绍,求恰好选中甲、乙两位同学的概率.

某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:.模拟驾驶;
.军事竞技;
.家乡导游;
.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任刘老师对全班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)八年级(3)班学生总人数是 ,并将条形统计图补充完整;
(2)刘老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这些学生中任意挑选两名担任活动记录员,请用列表或画树状图的方法,求恰好选中1名男生和1名女生担任活动记录员的概率.

某初中学校举行毛笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列问题:
(1)请将条形统计图补全;
(2)获得一等奖的同学中有来自七年级,有
来自八年级,其他同学均来自九年级,现准备从获得一等奖的同学中任选两人参加市内毛笔书法大赛,请通过列表或画树状图求所选出的两人中既有七年级又有九年级同学的概率.

中央电视台的"中国诗词大赛"节目文化品位高,内容丰富.某校初二年级模拟开展"中国诗词大赛"比赛,对全年级同学成绩进行统计后分为"优秀"、"良好"、"一般"、"较差"四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中"优秀"所对应扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学获得满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的"中国诗词大赛"比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
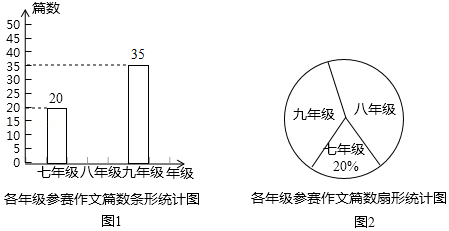
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用、
表示.若
为奇数,则甲获胜;若
为偶数,则乙获胜.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,求所有可能出现的结果总数;
(2)你认为这个游戏对双方公平吗?请说明理由.
将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其他方面完全相同,若背面向上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面向上放在桌面上,从中先随机抽取一张卡片,记该卡片上的数字为,再把剩下的两张卡片洗匀后,背面向上放在桌面上,再从这两张卡片中随机抽取一张卡片,记该卡片上的数字为
.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,写出所有可能出现的结果.
(2)求取出的两张卡片上的数字之和为偶数的概率.
数学课上,李老师准备了四张背面看上去无差别的卡片,
,
,
,每张卡片的正面标有字母
,
,
表示三条线段(如图),把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.
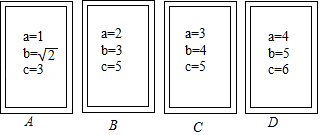
(1)用树状图或者列表表示所有可能出现的结果;
(2)求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
为了促进“足球进校园”活动的开展,某市举行了中学生足球比赛活动.现从,
,
三支获胜足球队中,随机抽取两支球队分别到两所边远地区学校进行交流.
(1)请用列表或画树状图的方法(只选择其中一种),表示出抽到的两支球队的所有可能结果;
(2)求出抽到队和
队参加交流活动的概率.
在一个不透明的盒子中,装有3个分别写有数字6,,7的小球,他们的形状、大小、质地完全相同,搅拌均匀后,先从盒子里随机抽取1个小球,记下小球上的数字后放回盒子,搅拌均匀后再随机取出1个小球,再记下小球上的数字.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,写出所有可能出现的结果;
(2)求两次取出的小球上的数字相同的概率.
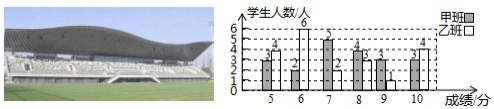
中华人民共和国第二届青年运动会(简称二青会)将于2019年8月在山西举行.太原市作为主赛区,将承担多项赛事,现正从某高校的甲、乙两班分别招募10人作为颁奖礼仪志愿者,同学们踊跃报名,甲、乙两班各报了20人,现已对他们进行了基本素质测评,满分10分.各班按测评成绩从高分到低分的顺序各录用10人,对这次基本素质测评中甲、乙两班学生的成绩绘制了如图所示的统计图.请解答下列问题:
(1)甲班的小华和乙班的小丽基本素质测评成绩都为7分,请你分别判断小华,小丽能否被录用(只写判断结果,不必写理由).
(2)请你对甲、乙两班各被录用的10名志愿者的成绩作出评价(从“众数”,“中位数”,或“平均数”中的一个方面评价即可).
(3)甲、乙两班被录用的每一位志愿者都将通过抽取卡片的方式决定去以下四个场馆中的两个场馆进行颁奖礼仪服务,四个场馆分别为:太原学院足球场,太原市沙滩排球场,山西省射击射箭训练基地,太原水上运动中心,这四个场馆分别用字母,
,
,
表示.现把分别印有
,
,
,
的四张卡片(除字母外,其余都相同)背面朝上,洗匀放好.志愿者小玲从中随机抽取一张(不放回),再从中随机抽取一张,请你用列表或画树状图的方法求小玲抽到的两张卡片恰好是“
”和“
”的概率.
从共享单车,共享汽车等共享出行到共享充电宝,共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者.根据国家信息中心发布的《中国分享经济发展报告2017》显示,2016年我国共享经济市场交易额约为34520亿元,比上年增长;超6亿人参与共享经济活动,比上年增加约1亿人.
如图是源于该报告中的中国共享经济重点领域市场规模统计图:
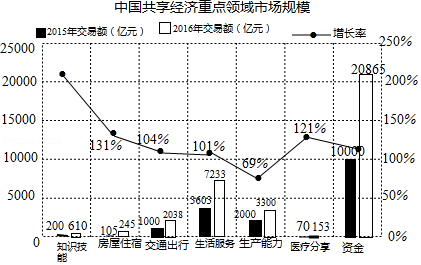
(1)请根据统计图解答下列问题:
①图中涉及的七个重点领域中,2016年交易额的中位数是 2038 亿元.
②请分别计算图中的“知识技能”和“资金”两个重点领域从2015年到2016年交易额的增长率(精确到,并就这两个重点领域中的一个分别从交易额和增长率两个方面,谈谈你的认识.
(2)小宇和小强分别对共享经济中的“共享出行”和“共享知识”最感兴趣,他们上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为,
,
,
的四张卡片(除编号和内容外,其余完全相同)他们将这四张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号
,
,
,
表示)
现有、
两个不透明袋子,分别装有3个除颜色外完全相同的小球.其中,
袋装有2个白球,1个红球;
袋装有2个红球,1个白球.
(1)将袋摇匀,然后从
袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的,
两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平.