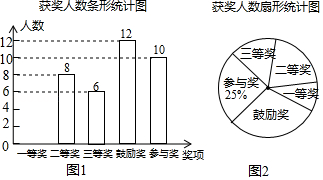
某初中学校举行毛笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列问题:
(1)请将条形统计图补全;
(2)获得一等奖的同学中有来自七年级,有来自八年级,其他同学均来自九年级,现准备从获得一等奖的同学中任选两人参加市内毛笔书法大赛,请通过列表或画树状图求所选出的两人中既有七年级又有九年级同学的概率.
推荐套卷
某初中学校举行毛笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列问题:
(1)请将条形统计图补全;
(2)获得一等奖的同学中有来自七年级,有来自八年级,其他同学均来自九年级,现准备从获得一等奖的同学中任选两人参加市内毛笔书法大赛,请通过列表或画树状图求所选出的两人中既有七年级又有九年级同学的概率.
