初中数学列表法与树状图法试题

在一个不透明的布袋里，装有完全相同的3个小球，小球上分别标有数字1，2，5；先从袋子里任意摸出1个球，记其标有的数字为 $x$，不放回；再从袋子里任意摸出一个球，记其标有的数字为 $y$，依次确定有理数 $\frac{x}{y}$．

（1）请用画树状图或列表的方法，写出 $\frac{x}{y}$的所有可能的有理数；

（2）求有理数 $\frac{x}{y}$为整数的概率．

一个不透明的袋子中有三个完全相同的小球，把它们分别标号为1，2，3，随机摸出一个小球，记下标号后放回，再随机摸出一个小球并记下标号，两次摸出的小球标号的和是偶数的概率是 $($　　 $)$

A． $\frac{1}{3}$B． $\frac{4}{9}$C． $\frac{1}{2}$D． $\frac{5}{9}$

有四张正面分别标有数字1，2， $-3$， $-4$的不透明卡片，它们除了数字之外其余全部相同，将它们背面朝上，洗匀后从四张卡片中随机地抽取一张不放回，将该卡片上的数字记为 $m$，再随机地抽取一张，将卡片上的数字记为 $n$．

（1）请用画树状图或列表法写出 $(m,n)$所有的可能情况；

（2）求所选的 $m$， $n$能使一次函数 $y=\mathit{mx}+n$的图象经过第一、三、四象限的概率．

某校在宣传“民族团结”活动中，采用四种宣传形式： $A$．器乐， $B$．舞蹈， $C$．朗诵， $D$．唱歌．每名学生从中选择并且只能选择一种最喜欢的，学校就宣传形式对学生进行了抽样调查，并将调查结果绘制了如下两幅不完整的统计图．

请结合图中所给信息，解答下列问题：

（1）本次调查的学生共有　　人；

（2）补全条形统计图；

（3）该校共有1200名学生，请估计选择“唱歌”的学生有多少人？

（4）七年一班在最喜欢“器乐”的学生中，有甲、乙、丙、丁四位同学表现优秀，现从这四位同学中随机选出两名同学参加学校的器乐队，请用列表或画树状图法求被选取的两人恰好是甲和乙的概率．

某校举办学生综合素质大赛，分“单人项目”和“双人项目”两种形式，比赛题目包括下列五类： $A$．人文艺术； $B$．历史社会； $C$．自然科学； $D$．天文地理； $E$．体育健康．

（1）若小明参加“单人项目”，他从中抽取一个题目，那么恰好抽中“自然科学”类题目的概率为　　．

（2）小林和小丽参加“双人项目”，比赛规定：同一小组的两名同学的题目类型不能相同，且每人只能抽取一次，求他们抽到“天文地理”和“体育健康”类题目的概率是多少？（用画树状图或列表的方法求解）

为了树立文明乡风，推进社会主义新农村建设，某村决定组建村民文体团队，现围绕“你最喜欢的文体活动项目（每人仅限一项）”，在全村范围内随机抽取部分村民进行问卷调查，并将调查结果绘制成如下两幅不完整的统计图．请你根据统计图解答下列问题：

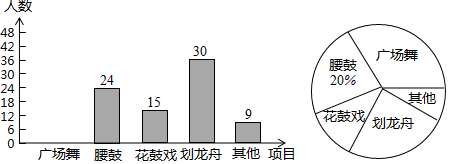
（1）这次参与调查的村民人数为　　人；

（2）请将条形统计图补充完整；

（3）求扇形统计图中“划龙舟”所在扇形的圆心角的度数；

（4）若在“广场舞、腰鼓、花鼓戏、划龙舟”这四个项目中任选两项组队参加端午节庆典活动，请用列表或画树状图的方法，求恰好选中“花鼓戏、划龙舟”这两个项目的概率．

永州植物园“清风园”共设11个主题展区．为推进校园文化建设，某校九年级（1）班组织部分学生到“清风园”参观后，开展“我最喜欢的主题展区”投票调查．要求学生从“和文化”、“孝文化”、“德文化”、“理学文化”、“瑶文化”五个展区中选择一项，根据调查结果绘制出了两幅不完整的条形统计图和扇形统计图．结合图中信息，回答下列问题．

（1）参观的学生总人数为　　人；

（2）在扇形统计图中最喜欢“瑶文化”的学生占参观总学生数的百分比为　　；

（3）补全条形统计图；

（4）从最喜欢“德文化”的学生中随机选两人参加知识抢答赛，最喜欢“德文化”的学生甲被选中的概率为　　．

2018年5月18日，益阳新建西流湾大桥竣工通车，如图，从沅江 $A$地到资阳 $B$地有两条路线可走，从资阳 $B$地到益阳火车站可经会龙山大桥或西流湾大桥或龙洲大桥到达，现让你随机选择一条从沅江 $A$地出发经过资阳 $B$地到达益阳火车站的行走路线，那么恰好选到经过西流湾大桥的路线的概率是　　．

为进一步深化基础教育课程改革，构建符合素质教育要求的学校课程体系，某学校自主开发了 $A$书法、 $B$阅读， $C$足球， $D$器乐四门校本选修课程供学生选择，每门课程被选到的机会均等．

（1）学生小红计划选修两门课程，请写出她所有可能的选法；

（2）若学生小明和小刚各计划选修一门课程，则他们两人恰好选修同一门课程的概率为多少？

从2018年高中一年级学生开始，湖南省全面启动高考综合改革，学生学习完必修课程后，可以根据高校相关专业的选课要求和自身兴趣、志向、优势，从思想政治、历史、地理、物理、化学、生物6个科目中，自主选择3个科目参加等级考试．学生 $A$已选物理，还从思想政治、历史、地理3个文科科目中选1科，再从化学、生物2个理科科目中选1科．若他选思想政治、历史、地理的可能性相等，选化学、生物的可能性相等，则选修地理和生物的概率为　　．

“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，根据测试成绩（成绩都不低于50分）绘制出如图所示的部分频数分布直方图．

请根据图中信息完成下列各题．

（1）将频数分布直方图补充完整人数；

（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少；

（3）现将从包括小明和小强在内的4名成绩优异的同学中随机选取两名参加市级比赛，求小明与小强同时被选中的概率．

某校体育组为了解全校学生“最喜欢的一项球类项目”，随机抽取了部分学生进行调查，下面是根据调查结果绘制的不完整的统计图．请你根据统计图回答下列问题：

（1）喜欢乒乓球的学生所占的百分比是多少？并请补全条形统计图（图 $2)$；

（2）请你估计全校500名学生中最喜欢“排球”项目的有多少名？

（3）在扇形统计图中，“篮球”部分所对应的圆心角是多少度？

（4）篮球教练在制定训练计划前，将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈，请用列表法或树状图法求抽取的两人恰好是甲和乙的概率．

三名初三学生坐在仅有的三个座位上，起身后重新就坐，恰好有两名同学没有坐回原座位的概率为 $($　　 $)$

A． $\frac{1}{9}$B． $\frac{1}{6}$C． $\frac{1}{4}$D． $\frac{1}{2}$

为了传承中华优秀传统文化，市教育局决定开展“经典诵读进校园”活动，某校团委组织八年级100名学生进行“经典诵读”选拔赛，赛后对全体参赛学生的成绩进行整理，得到下列不完整的统计图表．

组别	分数段	频次	频率
$A$	$60⩽x<70$	17	0.17
$B$	$70⩽x<80$	30	$a$
$C$	$80⩽x<90$	$b$	0.45
$D$	$90⩽x<100$	8	0.08

请根据所给信息，解答以下问题：

（1）表中 $a=$　　， $b=$　　；

（2）请计算扇形统计图中 $B$组对应扇形的圆心角的度数；

（3）已知有四名同学均取得98分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加市级比赛，请用列表法或画树状图法求甲、乙两名同学都被选中的概率．

某校高一年级今年计划招四个班的新生，并采取随机摇号的方法分班，小明和小红既是该校的高一新生，又是好朋友，那么小明和小红分在同一个班的机会是 $($　　 $)$

A． $\frac{1}{4}$B． $\frac{1}{3}$C． $\frac{1}{2}$D． $\frac{3}{4}$